某人乘车从A地到B地,所需时间(分钟)服从正态分布N(30,100),求此人在40分钟至50分钟到达目的地的概率.
设函数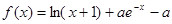 ,
,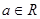 .
.
(Ⅰ)当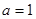 时,证明
时,证明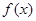 在
在 是增函数;
是增函数;
(Ⅱ)若 ,
,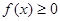 ,求
,求 的取值范围.
的取值范围.
如图椭圆 的右顶点是
的右顶点是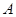 ,上下两个顶点分别为
,上下两个顶点分别为 ,四边形
,四边形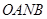 是矩形(
是矩形( 为原点),点
为原点),点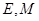 分别为线段
分别为线段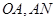 的中点.
的中点.
(Ⅰ)证明:直线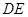 与直线
与直线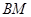 的交点在椭圆
的交点在椭圆 上;
上;
(Ⅱ)若过点 的直线交椭圆于
的直线交椭圆于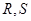 两点,
两点,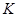 为
为 关于
关于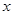 轴的对称点(
轴的对称点(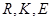 不共线),问:直线
不共线),问:直线 是否经过
是否经过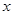 轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.
轴上一定点,如果是,求这个定点的坐标,如果不是,说明理由.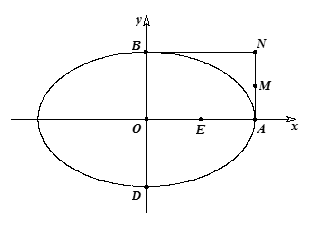
现有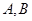 两个项目,投资
两个项目,投资 项目
项目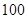 万元,一年后获得的利润为随机变量
万元,一年后获得的利润为随机变量 (万元),根据市场分析,
(万元),根据市场分析, 的分布列为:
的分布列为:
| X1 |
12 |
11.8 |
11.7 |
| P |
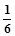 |
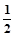 |
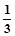 |
投资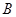 项目
项目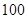 万元,一年后获得的利润
万元,一年后获得的利润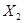 (万元)与
(万元)与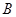 项目产品价格的调整(价格上调或下调)有关, 已知
项目产品价格的调整(价格上调或下调)有关, 已知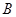 项目产品价格在一年内进行
项目产品价格在一年内进行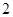 次独立的调整,且在每次调整中价格下调的概率都是
次独立的调整,且在每次调整中价格下调的概率都是 .
.
经专家测算评估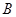 项目产品价格的下调与一年后获得相应利润的关系如下表:
项目产品价格的下调与一年后获得相应利润的关系如下表:
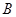 项目产品价格一年内下调次数 项目产品价格一年内下调次数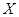 (次) (次) |
 |
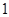 |
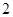 |
投资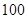 万元一年后获得的利润 万元一年后获得的利润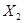 (万元) (万元) |
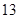 |
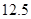 |
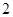 |
(Ⅰ)求 的方差
的方差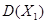 ;
;
(Ⅱ)求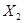 的分布列;
的分布列;
(Ⅲ)若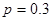 ,根据投资获得利润的差异,你愿意选择投资哪个项目?
,根据投资获得利润的差异,你愿意选择投资哪个项目?
(参考数据: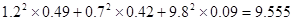 ).
).
如图,四边形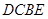 为直角梯形,
为直角梯形,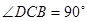 ,
,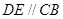 ,
,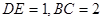 ,又
,又 ,
,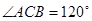 ,
,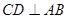 ,直线
,直线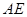 与直线
与直线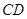 所成角为
所成角为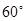 .
.
(Ⅰ)求证:平面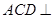 平面
平面 ;
;
(Ⅱ)求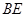 与平面
与平面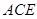 所成角的正弦值.
所成角的正弦值.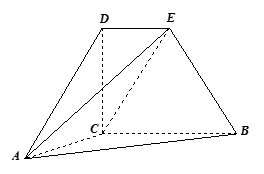
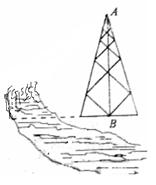
如图, 是底部
是底部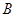 不可到达的一个塔型建筑物,
不可到达的一个塔型建筑物,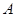 为塔的最高点.现需在对岸测出塔高
为塔的最高点.现需在对岸测出塔高 ,甲、乙两同学各提出了一种测量方法,甲同学的方法是:选与塔底
,甲、乙两同学各提出了一种测量方法,甲同学的方法是:选与塔底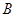 在同一水平面内的一条基线
在同一水平面内的一条基线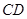 ,使
,使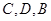 三点不在同一条直线上,测出
三点不在同一条直线上,测出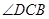 及
及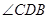 的大小(分别用
的大小(分别用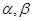 表示测得的数据)以及
表示测得的数据)以及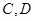 间的距离(用
间的距离(用 表示测得的数据),另外需在点
表示测得的数据),另外需在点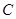 测得塔顶
测得塔顶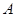 的仰角(用
的仰角(用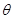 表示测量的数据),就可以求得塔高
表示测量的数据),就可以求得塔高 .乙同学的方法是:选一条水平基线
.乙同学的方法是:选一条水平基线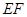 ,使
,使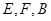 三点在同一条直线上.在
三点在同一条直线上.在 处分别测得塔顶
处分别测得塔顶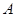 的仰角(分别用
的仰角(分别用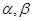 表示测得的数据)以及
表示测得的数据)以及 间的距离(用
间的距离(用 表示测得的数据),就可以求得塔高
表示测得的数据),就可以求得塔高 .请从甲或乙的想法中选出一种测量方法,写出你的选择并按如下要求完成测量计算:①画出测量示意图;②用所叙述的相应字母表示测量数据,画图时
.请从甲或乙的想法中选出一种测量方法,写出你的选择并按如下要求完成测量计算:①画出测量示意图;②用所叙述的相应字母表示测量数据,画图时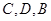 按顺时针方向标注,
按顺时针方向标注,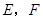 按从左到右的方向标注;③求塔高
按从左到右的方向标注;③求塔高 .
.