已知二次函数
为常数）；
.若直线l1、l2与函数f（x）的图象以及l1，y轴与函数f（x）的图象所围成的封闭图形如阴影所示.
（Ⅰ）求a、b、c的值；
（Ⅱ）求阴影面积S关于t的函数S（t）的解析式；
（Ⅲ）若
问是否存在实数m，使得y=f（x）的图象与y=g（x）的图象有且只有两个不同的交点？若存在，求出m的值；若不存在，说明理由.
已知函数
，函数
.
（1）当
时，求函数f(x)的最小值；
（2）设函数h(x)=(1－x)f(x)+16，试根据m的取值分析函数h(x)的图象与函数g(x)的图象交点的个数.
设函数
（1）求函数f(x)的单调区间，并求函数f(x)的极大值和极小值；
（2）当x∈[a+1, a+2]时，不等
，求a的取值范围.
已知函数f（x）＝ax2＋bx＋c，其中a∈N*，b∈N，c∈Z。
（1）若b>2a，且f（sinx）（x∈R）的最大值为2，最小值为－4，试求函数f（x）的最小值；
（2）若对任意实数x，不等式4x≤f（x）≤2（x2＋1）恒成立，且存在x0，使得f（x0）<2（x02＋1）成立，求c的值。
设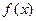
是定义域在
上的奇函数，且其图象上任意两点连线的斜率均小于零.
（l）求证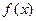在上是减函数；
（ll）如果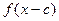
，
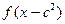的定义域的交集为空集，求实数
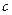的取值范围；
（lll）证明若
，则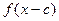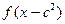，存在公共的定义域，并求这个公共的空义域.