据行业协会预测:某公司以每吨10万元的价格销售某种化工产品,可售出该产品1000吨,若将该产品每吨的价格上涨 ,则销售量将减少
,则销售量将减少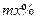 ,且该化工产品每吨的价格上涨幅度不超过
,且该化工产品每吨的价格上涨幅度不超过 ,(其中
,(其中 为正常数)
为正常数)
(1)当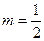 时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
时,该产品每吨的价格上涨百分之几,可使销售的总金额最大?
(2)如果涨价能使销售总金额比原销售总金额多,求 的取值范围.
的取值范围.
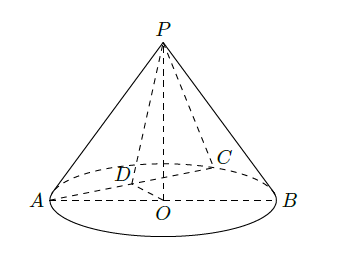
如图,在圆锥
中,已知
,
的直径
,点
在
上,且
,
为
的中点.
(I)证明:
(II)求直线和平面 所成角的正弦值.
某河流上的一座水力发电站,每年六月份的发电量
(单位:万千瓦时)与该河上游在六月份的降雨量
(单位:毫米)有关.据统计,当
时,
;
每增加10,
增 加5;已知近20年
的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
加5;已知近20年
的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
(I)完成如下的频率分布表:
近20年六月份降雨量频率分布表
| 降雨量 |
70 |
 110 110 |
140 |
160 |
200 |
220 |
| 频率 |
(II)假定今年六月份的降雨量与近20年六月份的降雨量的分布规律相同,并将频率视为概率,求今 年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.
年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.
在 中,角 所对的边分别为 且满足 .
(I)求角
的大小;
(II)求
的最大值,并求取得最大值时角
的大小.
在数1和100之间插入
个实数,使得这
个数构成递增的等比数列,将这
个数的乘 积记作
,再令
,
.
积记作
,再令
,
.
(Ⅰ)求数列
的通项公式;
(Ⅱ)设
,求数列
的前
项和
.
某地最近十年粮食需求量逐年上升, 下表是
下表是 部分统计数据:
部分统计数据:
| 年份 |
2002 |
2004 |
2006 |
2008 |
2010 |
| 需求量(万吨) |
236 |
246 |
257 |
276 |
286 |
(Ⅰ)利用所给数据求年需求量与年份之间的回归直线方程 ;
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地2012年的粮食需求量。
温馨提示:答题前请仔细阅读卷首所给的计算公式及说明.