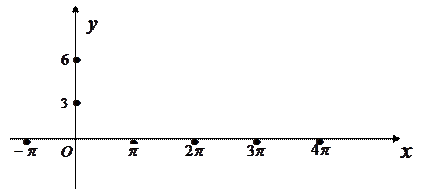某河流上的一座水力发电站,每年六月份的发电量
(单位:万千瓦时)与该河上游在六月份的降雨量
(单位:毫米)有关.据统计,当
时,
;
每增加10,
增 加5;已知近20年
的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
加5;已知近20年
的值为:140,110,160,70,200,160,140,160,220,200,110,160,160,200,140,110,160,220,140,160.
(I)完成如下的频率分布表:
近20年六月份降雨量频率分布表
| 降雨量 |
70 |
 110 110 |
140 |
160 |
200 |
220 |
| 频率 |
(II)假定今年六月份的降雨量与近20年六月份的降雨量的分布规律相同,并将频率视为概率,求今 年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.
年六月份该水力发电站的发电量低于490(万千瓦时)或超过530(万千瓦时)的概率.
(本小题满分14分)
已知向量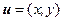 与向量
与向量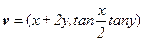 的对应关系可用
的对应关系可用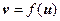 表示.试问是否存在向量
表示.试问是否存在向量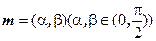 ,使得
,使得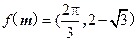 成立?如果存在,求出向量
成立?如果存在,求出向量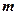 ;如果不存在,请说明理由.
;如果不存在,请说明理由.
(本小题满分12分)
已知向量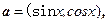
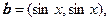
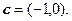
(1)若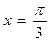 ,求向量
,求向量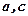 的夹角;
的夹角;
(2)(2)若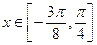 ,求函数
,求函数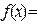
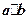 的最值以及相应的
的最值以及相应的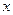 的值.
的值.
(本小题满分12分)
已知函数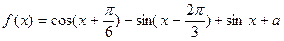 的最大值为
的最大值为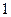 .
.
(1)求常数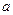 的值;
的值;
(2)求使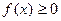 成立的
成立的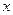 的取值范围.
的取值范围.
(本小题满分12分)
已知向量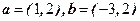 .
.
(1)求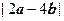 ;
;
(2)若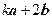 与
与 平行,求
平行,求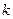 的值;
的值;
(3)若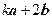 与
与 的夹角是钝角,求实数
的夹角是钝角,求实数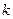 的取值范围.
的取值范围.
(本小题满分12分)
已知函数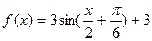 .
.
(1)用五点法画出它在一个周期内的闭区间上的图象;
(2)指出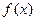 的周期、振幅、初相、对称轴;
的周期、振幅、初相、对称轴;
(3)写出函数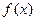 的单调递增区间.
的单调递增区间.