在中,内角的对边分别为,已知.
(Ⅰ)求的值;
(Ⅱ)的值.
一条双曲线
的左、右顶点分别为
,点
是双曲线上不同的两个动点.
(1)求直线
与
交点的轨迹
的方程式;
(2)若过点
的两条直线
和
与轨迹
都只有一个交点,且
,求
的值.
某营养师要为某个儿童预定午餐和晚餐。已知一个单位的午餐含12个单位的碳水化合物6个单位蛋白质和6个单位的维生素
;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素
.另外,该儿童这两餐需要的营养 中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素
.
中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素
.
如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预定多少个单位的午餐和晚餐?
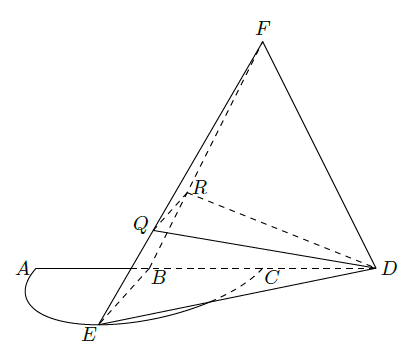
如图,
是半径为
的半圆,
为直径,点
为
的中点,点
和点
为线段
的三等分点.平面
外一点
满足
,
. 
(1)证明:
;
(2)已知点
分别为线段
上的点,使得
,
,求平面
与平面
所成二面角的正弦值.
某食品厂为了检查一条自动包装流水线的生产情况,随即抽取该流水线上40件产品作为样本算出他们的重量(单位:克)重量的分组区间为
,
,……
,由此得到样本的频率分布直方图,如图所示. 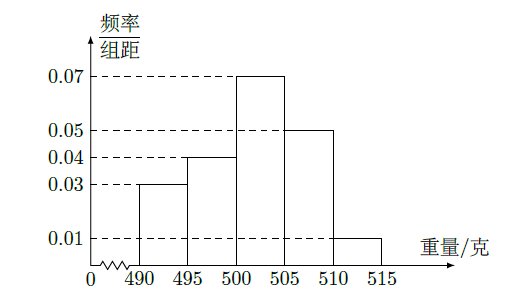
(1)根据频率分布直方图,求重量超过505克的产品数量.
(2)在上述抽取的40件产品中任取2件,设Y为重量超过505克的产品数量,求Y的分布列.
(3)从流水线上任取5件产品,求恰有2件产品合格的重量超过505克的概率.
已知函数
在
时取得最大值4.
(1)求
的最小正周期;
(2)求
的解析式;
(3)若
,求
.