如图所示,圆O的两弦AB和CD交于点E,
EF∥CB,EF交AD的延长线于点F,FG切圆O于点G.
(1)求证:△DFE∽△EFA;
(2)如果EF=1,求FG的长.
如图,两块直角三角板拼在一起,已知 ,
, .
.
(1)若记 ,
, ,试用
,试用 ,
, 表示向量
表示向量 、
、 ;
;
(2)若 ,求
,求
 .
.
已知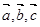 在同一平面内,且
在同一平面内,且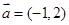 .
.
(1)若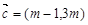 ,且
,且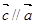 ,求
,求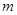 的值;
的值;
(2)若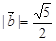 ,且
,且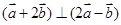 ,求向量
,求向量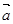 与
与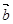 的夹角.
的夹角.
一只不透明的袋子中装有颜色分别为红、黄、蓝、白的球各一个,这些球除颜色外都相同.
(1)求搅匀后从中任意摸出1个球,恰好是红球的概率;
(2)搅匀后从中任意摸出1个球,记录下颜色后放回袋子中并搅匀,再从中任意摸出1个球,求至少有一次摸出的球是红球的概率.
在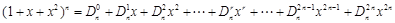 的展开式中,把
的展开式中,把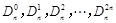 叫做三项式系数.
叫做三项式系数.
(1)当n=2时,写出三项式系数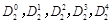 的值;
的值;
(2)类比二项式系数性质
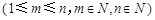 ,给出一个关于三项式系数
,给出一个关于三项式系数 的相似性质,并予以证明;
的相似性质,并予以证明;
(3)求 的值.
的值.
如图,已知正四棱锥 的底面边长为2,高为
的底面边长为2,高为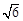 ,P是棱SC的中点.
,P是棱SC的中点.
(1)求直线AP与平面SBC所成角的正弦值;
(2)求二面角B-SC-D大小的余弦值;
(3)在正方形ABCD内是否存在一点Q,使得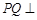 平面SDC?若存在,求PQ的长;若不存在,请说明理由.
平面SDC?若存在,求PQ的长;若不存在,请说明理由.