试求曲线y=sinx在矩阵MN变换下的函数解析式,其中M= ,N=
,N= .
.
已知函数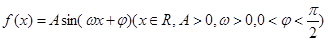 的部分图象如图所示,
的部分图象如图所示,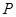 是图象的最高点,
是图象的最高点,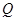 为图象与
为图象与 轴的交点,
轴的交点, 为坐标原点,若
为坐标原点,若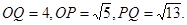
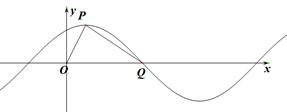
(1)求函数 的解析式,
的解析式,
(2)将函数 的图象向右平移2个单位后得到函数
的图象向右平移2个单位后得到函数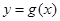 的图象,当
的图象,当 时,求函数
时,求函数 的值域.
的值域.
已知函数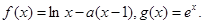
(1)求函数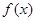 的单调区间;
的单调区间;
(2)当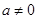 时,过原点分别作曲线
时,过原点分别作曲线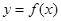 和
和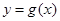 的切线
的切线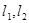 ,已知两切线的斜率互为倒数,证明:
,已知两切线的斜率互为倒数,证明: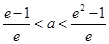 ;
;
(3)设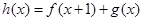 ,当
,当 时,求实数
时,求实数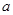 的取值范围.
的取值范围.
(本小题满分14分)已知椭圆 (
(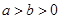 )的左、右顶点分别为
)的左、右顶点分别为 ,
, ,
,
且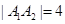 ,
, 为椭圆上异于
为椭圆上异于 ,
, 的点,
的点, 和
和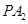 的斜率之积为
的斜率之积为 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)设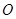 为椭圆中心,
为椭圆中心, ,
, 是椭圆上异于顶点的两个动点,求
是椭圆上异于顶点的两个动点,求 面积的最大值.
面积的最大值.
翡翠市场流行一种赌石“游戏规则”:翡翠在开采出来时有一层风化皮包裹着,无法知道其内的好坏,需切割后方能知道翡翠的价值,参加者先缴纳一定金额后可得到一块翡翠石并现场开石验证其具有的收藏价值,其举办商在赌石游戏中设置了甲乙两种赌石规则,规则甲的赌中率为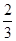 ,赌中后可获得20万元;规则乙的赌中率为
,赌中后可获得20万元;规则乙的赌中率为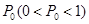 ,赌中后可获得30万元;未赌中则没有收获,每人有且只有一次赌石机会,每次赌中与否互不影响,赌石结束后当场得到兑现金额.
,赌中后可获得30万元;未赌中则没有收获,每人有且只有一次赌石机会,每次赌中与否互不影响,赌石结束后当场得到兑现金额.
(1)收藏者张先生选择规则甲赌石,收藏者李先生选择规则乙赌石,记他们的累计获得金额数为 (单位:万元),若
(单位:万元),若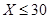 的概率为
的概率为 ,求
,求 的大小;
的大小;
(2)若收藏者张先生李先生都选择赌石规则甲或赌石规则乙进行赌石,问:他们选择何种规则赌石,累积得到的金额的数学期望最大?
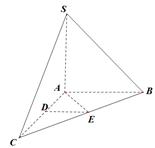
如图,在三棱锥 中,
中, 底面
底面 ,
, ,
,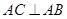 ,
,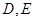 分别是
分别是 的中点,
的中点, 在
在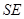 上,且
上,且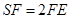 .
.
(1)求证: 平面
平面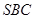 ;
;
(2)在线段上 上是否存在点
上是否存在点 ,使二面角
,使二面角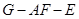 的大小为
的大小为 ?若存在,求出
?若存在,求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.