已知二阶矩阵M有特征值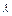 =8及对应的一个特征向量e1=
=8及对应的一个特征向量e1=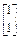 ,并且矩阵M对应的变换将点(-1,2)变换成(-2,4).求直线l:x-y+1=0在矩阵M的变换下的直线l′的方程.
,并且矩阵M对应的变换将点(-1,2)变换成(-2,4).求直线l:x-y+1=0在矩阵M的变换下的直线l′的方程.
已知在四棱锥 中,底面
中,底面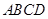 是矩形,且
是矩形,且 ,
, ,
, 平面
平面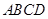 ,
, 、
、 分别是线段
分别是线段 、
、 的中点.
的中点.
(1)证明: ;
;
(2)判断并说明 上是否存在点
上是否存在点 ,使得
,使得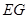 ∥平面
∥平面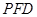 ;
;
(3)若 与平面
与平面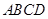 所成的角为
所成的角为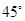 ,求二面角
,求二面角 的余弦值.
的余弦值.
某市第一中学要用鲜花布置花圃中 五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
五个不同区域,要求同一区域上用同一种颜色的鲜花,相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择.
(1)当 区域同时用红色鲜花时,求布置花圃的不同方法的种数;
区域同时用红色鲜花时,求布置花圃的不同方法的种数;
(2)求恰有两个区域用红色鲜花的概率;
(3)记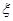 为花圃中用红色鲜花布置的区域的个数,求随机变量
为花圃中用红色鲜花布置的区域的个数,求随机变量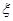 的分布列及其数学期望.
的分布列及其数学期望.
在△ABC中,角A、B、C的对边分别为a、b、c.已知a+b=5,c = ,且
,且
(1)求角C的大小;
(2)求△ABC的面积.
已知函数 .
.
(1)当 时,求函数
时,求函数 的极值点;
的极值点;
(2)记 ,若对任意
,若对任意 ,都有
,都有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知 满足
满足 ,
, ,
,
(1)求 ,并猜想
,并猜想 的表达式;
的表达式;
(2)用数学归纳法证明对 的猜想.
的猜想.