已知在四棱锥 中,底面
中,底面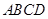 是矩形,且
是矩形,且 ,
, ,
, 平面
平面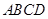 ,
, 、
、 分别是线段
分别是线段 、
、 的中点.
的中点.
(1)证明: ;
;
(2)判断并说明 上是否存在点
上是否存在点 ,使得
,使得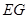 ∥平面
∥平面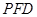 ;
;
(3)若 与平面
与平面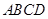 所成的角为
所成的角为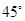 ,求二面角
,求二面角 的余弦值.
的余弦值.
甲乙丙丁4人玩传球游戏,持球者将球等可能的传给其他3人,若球首先从甲传出,经过3次传球.
(1)求球恰好回到甲手中的概率;
(2)设乙获球(获得其他游戏者传的球)的次数为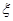 ,求
,求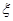 的分布列及数学期望.
的分布列及数学期望.
如图,△ABC中.角A、B、C所对边的长分别为a、b、c满足c=l, 以AB为边向△ABC外作等边三角形△ABD.
以AB为边向△ABC外作等边三角形△ABD.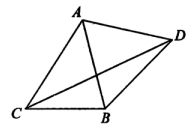
(1)求∠ACB的大小;
(2)设∠ABC=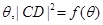 .试求函数
.试求函数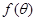 的最大值及
的最大值及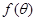 取得最大值时的
取得最大值时的 的值.
的值.
已知 .
.
(1)当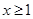 时,求
时,求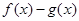 的最大值;
的最大值;
(2)求证: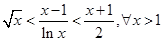 恒成立;
恒成立;
(3)求证: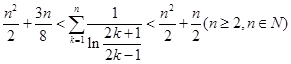 .(参考数据:
.(参考数据: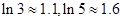 )
)
已知椭圆C的两个焦点是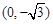 )和
)和 ,并且经过点
,并且经过点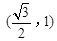 ,抛物线的顶点E在坐标原点,焦点恰好是椭圆C的右顶点F.
,抛物线的顶点E在坐标原点,焦点恰好是椭圆C的右顶点F.
(1)求椭圆C和抛物线E的标准方程;
(2)过点F作两条斜率都存在且互相垂直的直线l1、l2,l1交抛物线E于点A、B,l2交抛物线E于点G、H,求 的最小值.
的最小值.
设函数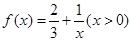 ,数列
,数列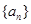 满足
满足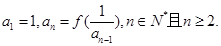
(1)求数列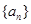 的通项公式;
的通项公式;
(2)对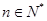 ,设
,设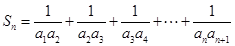 ,若
,若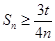 恒成立,求实数
恒成立,求实数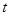 的取值范围.
的取值范围.