某商品在近30天内每件的销售价格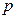 (元)与时间
(元)与时间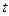 (天)的函数关系是
(天)的函数关系是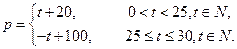 该商品的日销售量
该商品的日销售量 (件)与时间
(件)与时间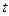 (天)的函数关系是
(天)的函数关系是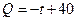
 ,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几
,求这种商品的日销售金额的最大值,并指出日销售金额最大的一天是30天中的第几 天?
天?
已知函数
⑴ 判断函数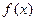 的单调性,并利用单调性定义证
的单调性,并利用单调性定义证 明;
明;
⑵ 求函数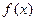 的最大值和最小值
的最大值和最小值
(每小题5分,共10分)计算下列各式的值:
(1) ; (2)
; (2) 
(本题满分18分,第(1)小题4分,第(2)小题6分,第(3)小题8分)
对于数列 ,如果存在一个正整数
,如果存在一个正整数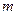 ,使得对任意的
,使得对任意的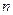 (
( )都有
)都有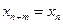 成立,那么就把这样一类数列
成立,那么就把这样一类数列 称作周期为
称作周期为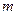 的周期数列,
的周期数列,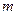 的最小值称作数列
的最小值称作数列 的最小正周期,以下简称周期。例如当
的最小正周期,以下简称周期。例如当 时
时 是周期为
是周期为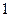 的周期数列,当
的周期数列,当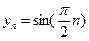 时
时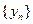 是周期为
是周期为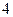 的周期数列。
的周期数列。
(1)设数列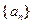 满足
满足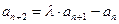 (
( ),
),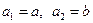 (
(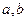 不同时为0),且数列
不同时为0),且数列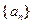 是周期为
是周期为 的周期数列,求常数
的周期数列,求常数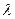 的值;
的值;
(2)设数列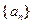 的前
的前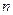 项和为
项和为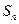 ,且
,且 .
.
①若 ,试判断数列
,试判断数列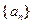 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
②若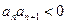 ,试判断数列
,试判断数列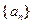 是否为周期数列,并说明理由;
是否为周期数列,并说明理由;
(3)设数列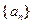 满足
满足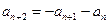 (
( ),
), ,
,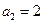 ,
,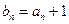 ,数列
,数列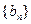 的前
的前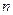 项和为
项和为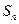 ,试问是否存在
,试问是否存在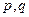 ,使对任意的
,使对任意的 都有
都有 成立,若存在,求出
成立,若存在,求出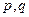 的取值范围;不存在,说明理由;
的取值范围;不存在,说明理由;
(本题满分16分,第(1)小题6分,第(2)小题10分)
设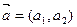 ,
, 定义一种向量的运算:
定义一种向量的运算: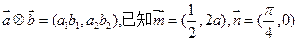 ,点P(x,y)在函数
,点P(x,y)在函数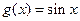 的图像上运动,点Q在
的图像上运动,点Q在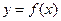 的图像上运动,且满足
的图像上运动,且满足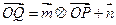 (其中O为坐标原点)
(其中O为坐标原点)
(1)求函数f(x)的解析式;
(2)若函数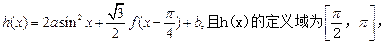 值域为
值域为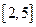 ,求a,b的值。
,求a,b的值。