已知抛物线 ,过点
,过点
 作直线
作直线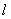 交抛物线于
交抛物线于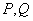 (点
(点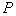 在第一象限);
在第一象限);
(1)设点 关于
关于 轴的对称点为
轴的对称点为 ,直线
,直线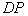 交
交 轴于点
轴于点 ,求证:
,求证: 为定点;
为定点;
(2)若 ,
, 为抛物线
为抛物线 上的三点,且
上的三点,且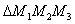 的重心为
的重心为 ,求线段
,求线段 所在直线的斜率的取值范围.
所在直线的斜率的取值范围.
(本小题满分13分)已知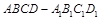 是边长为1的正方体,求:
是边长为1的正方体,求: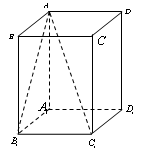
(Ⅰ)直线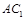 与平面
与平面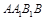 所成角的正切值;
所成角的正切值;
(Ⅱ)二面角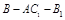 的大小.
的大小.
(本小题满分13分)
某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
| 组号 |
第一组 |
第二组 |
第三组 |
第四组 |
第五组 |
| 分组 |
[50,60) |
[60,70) |
[70,80) |
[80,90) |
[90,100] |
(Ⅰ)求图中a的值;
(Ⅱ)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均分;
(Ⅲ)现用分层抽样的方法从第3、4、5组中随机抽取6名学生,将该样本看成一个总体,从中随机抽取
2名,求其中恰有1人的分数不低于90分的概率?
(本小题满分12分)已知向量 ,
, ,其中
,其中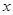 随机选自集合
随机选自集合 ,
, 随机选自集合
随机选自集合 ,
,
(Ⅰ)求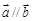 的概率;
的概率;
(Ⅱ)求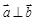 的概率.
的概率.
(满分14分)已知函数 ,(
,(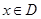 ),若同时满足以下条件:
),若同时满足以下条件:
① 在D上单调递减或单调递增;
在D上单调递减或单调递增;
②存在区间[ ]
] D,使
D,使 在[
在[ ]上的值域是[
]上的值域是[ ],那么称
],那么称 (
(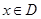 )为闭函数.
)为闭函数.
(1)求闭函数 符合条件②的区间[
符合条件②的区间[ ];
];
(2)判断函数
 是不是闭函数?若是请找出区间[
是不是闭函数?若是请找出区间[ ];若不是请说明理由;
];若不是请说明理由;
(3)若 是闭函数,求实数
是闭函数,求实数 的取值范围.
的取值范围.
(注:本题求解中涉及的函数单调性不用证明,直接指出是增还是减函数即可)
(满分14分)设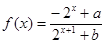 (
(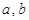 为实常数)。
为实常数)。
(1)当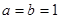 时,证明:①
时,证明:① 不是奇函数;
不是奇函数;
② 是
是 上的单调递减函数。
上的单调递减函数。
(2)设 是奇函数,求
是奇函数,求 与
与 的值。
的值。