(本小题12分)
已知曲线 直线
直线
 ,且直线
,且直线 与曲线
与曲线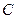
 相切于点
相切于点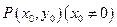 ,求直线
,求直线 的方程和切点
的方程和切点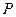 的坐标。
的坐标。
(本小题10分)
某工厂生产某种产品,已知该产品的月产量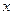 (吨)与每吨产品的价格
(吨)与每吨产品的价格 (元/吨)之间的关系为
(元/吨)之间的关系为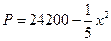 ,且生产
,且生产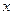 吨产品的成本为
吨产品的成本为 (元)。问该工厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?
(元)。问该工厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?
((本小题满分12分)
已知函数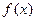 是
是 上的增函数,
上的增函数, ,
, .
.
(Ⅰ)若 ,求证:
,求证: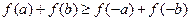 ;
;
(Ⅱ)判断(Ⅰ)中命题的逆命题是否成立,并用反证法证明你的结论.
((本小题共8分)
某公司做人事调整:设总经理一个,配有经理助理一名;设副经理两人,直接对总经理负责,设有6个部门,其中副经理A管理生产部、安全部和质量部,经理B管理销售部、财务部和保卫部;生产车间由生产部和安全部共同管理,公司配有质 检中心和门岗。请根据以上信息设计并画出该公司的人事结构图。
检中心和门岗。请根据以上信息设计并画出该公司的人事结构图。
(本小题共8分)
已知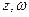 为复数,
为复数, 为纯虚数,
为纯虚数, ,且
,且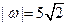 。求复数
。求复数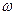 。
。