已知平面 ∥
∥ ,在
,在 内有4个点,在
内有4个点,在 内有6个点.
内有6个点.
(1)过这10个点中的3点作一平面,最多可作多少个不同平面?
(2)以这些点为顶点,最多可作多少个三棱锥?
(3)上述三棱锥中最多可以有多少个不同的体积?
某高速公路某施工工地需调运建材100吨,可租用装载的卡车和农用车分别为10辆和20辆,若每辆卡车装载8吨,运费960元,每辆农用车装载2.5吨,运费360元,问两种车各租用多少辆时,才能一次性装完且总费用最低?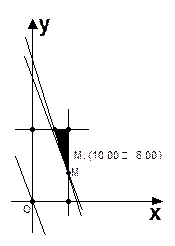
如图为函数y=Asin(ωx+φ)(A>0,ω>0)的图象的一部分,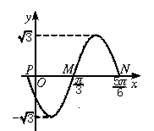
试求该函数的一个解析式.
已知数列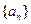 满足
满足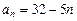 ,
,
(1)求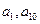 ;(2)判断20是不是这个数列的项,并说明理由; (3)求这个数列前n项的和
;(2)判断20是不是这个数列的项,并说明理由; (3)求这个数列前n项的和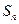 。
。
解不等式 >1的解集。
>1的解集。
在平面直角坐标系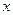 O
O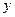 中,直线
中,直线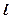 与抛物线
与抛物线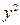 =2
=2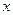 相交于A、B两点.
相交于A、B两点.
(1)求证:“如果直线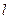 过点T(3,0),那么
过点T(3,0),那么
 =3”是真命题;
=3”是真命题;
(2)写出(1)中命题的逆命题,判断它是真命题还是假命题,并说明理由.