如图,已知四边形 与
与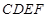 均为正方形,平面
均为正方形,平面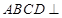 平面
平面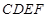 .
.
(1)求证: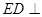 平面
平面 ;
;
(2)求二面角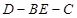 的大小.
的大小.
已知椭圆 :
: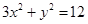 ,直线
,直线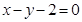 交椭圆
交椭圆 于
于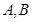 两点.
两点.
(Ⅰ)求椭圆 的焦点坐标及长轴长;
的焦点坐标及长轴长;
(Ⅱ)求以线段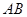 为直径的圆的方程.
为直径的圆的方程.
在打靶训练中,某战士射击一次的成绩在9环(包括9环)以上的概率是0.18,在8~9环(包括8环)的概率是0.51,在7~8环(包括7环)的概率是0.15,在6~7环(包括6环)的概率是0.09.计算该战士在打靶训练中射击一次取得8环(包括8环)以上成绩的概率和该战士打靶及格(及格指6环以上包括6环)的概率.
已知 为椭圆
为椭圆 上的三个点,
上的三个点, 为坐标原点.
为坐标原点.
(1)若 所在的直线方程为
所在的直线方程为 ,求
,求 的长;
的长;
(2)设 为线段
为线段 上一点,且
上一点,且 ,当
,当 中点恰为点
中点恰为点 时,判断
时,判断 的面积是否为常数,并说明理由.
的面积是否为常数,并说明理由.
已知抛物线 ,点
,点 ,过
,过 的直线
的直线 交抛物线
交抛物线 于
于 两点.
两点.
(1)若线段 中点的横坐标等于
中点的横坐标等于 ,求直线
,求直线 的斜率;
的斜率;
(2)设点 关于
关于 轴的对称点为
轴的对称点为 ,求证:直线
,求证:直线 过定点.
过定点.