(1)为了调查某班学生的身高情况，利用系统抽样的方法，样本容量为40.这个班共分5个组，每个组都有8名学生，他们的座次是按照个子高矮进行编排的.小王是这样做的，抽样距是8，按照每个小组的座次顺序进行编号，你觉得这样抽取的样本具有代表性吗？
(2)为了调查某路口一个月的交通流量情况，小刘采用系统抽样的方法，样本距为7，从每周中随机抽取一天，他正好抽取的是星期一，这样他每个星期一对这个路口的交通流量进行了统计，最后做出调查报告.你认为小刘这样的抽样方法有什么问题？应当怎样改进？
（本小题满分14分）
已知函数
（1）求f(x)在[0，1]上的极值；
（2）若对任意
成立，求实数a的取值范围；
（3）若关于x的方程
在[0，2]上恰有两个不同的实根,求实数b的取值范围.
（本小题满分13分）
过椭圆
内一点M(1，1)的弦AB
(1）若点M恰为弦AB的中点，求直线AB的方程；
（2）求过点M的弦的中点的轨迹方程。
（本小题满分13分）
数列
（I）求数列
的通项公式；
（II）若
的最大值。
（本小题满分13分）
已知三棱锥P－ABC中，PA⊥ABC，AB⊥AC，PA=AC=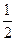
AB，N为AB上一点，AB=4AN,M,S分别为PB,BC的中点.
（Ⅰ）证明：CM⊥SN；
（Ⅱ）求SN与平面CMN所成角的大小.
（本小题满分13分）
已知
，
，f(x)=
⑴ 求f(x)的最小正周期和单调增区间；
⑵ 如果三角形ABC中，满足f(A)=
，求角A的值．