(本小题满分12分)
某食品企业一个月内被消费者投诉的次数用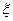 表示,据统计,随机变量
表示,据统计,随机变量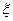 的概率分布如下:
的概率分布如下:
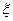 |
0 |
1 |
2 |
3 |
| p |
0.1 |
0.3 |
2a |
a |
(1)求a的值和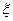 的数学期望;
的数学期望;
(2)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被
消费者投诉2次的概率.
其中第(1)(2)问文理科学生都要做,第(3)问按题目要求分文理来做。
已知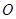 为坐标原点,向量
为坐标原点,向量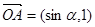 ,
,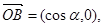
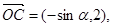 点
点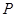 是直线
是直线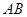 上的一点,且
上的一点,且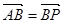 .
.
求点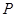 的坐标(用
的坐标(用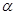 表示);
表示);
若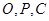 三点共线,求以线段
三点共线,求以线段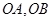 为邻边的平行四边形的对角线长;
为邻边的平行四边形的对角线长;
(3)(文科生做)记函数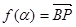 •
•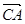 ,且
,且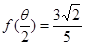 ,求
,求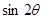 的值.
的值.
(3)(理科生做)记函数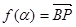 •
•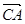 ,
,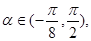 讨论函数
讨论函数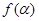 的单调性,并求其值域.
的单调性,并求其值域.
在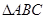 中,角
中,角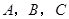 所对的边分别为
所对的边分别为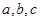 ,且
,且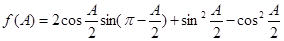
(1)求函数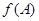 的最大值;
的最大值;
(2)若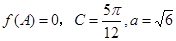 ,求
,求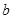 的值.
的值.
如图,在平行四边形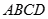 中,
中,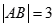 ,
, ,
,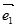 =
=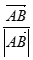 ,
,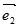 =
=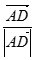 ,
,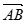 与
与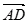 的夹角为
的夹角为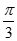 .
.
(1)若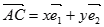 ,求
,求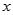 、
、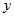 的值;
的值;
(2)求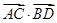 的值;
的值;
(3)求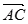 与
与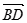 的夹角的余弦值.
的夹角的余弦值.
设函数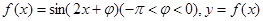 的图象的一条对称轴是直线
的图象的一条对称轴是直线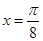 .
.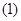 求
求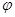 ;
;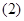 求函数
求函数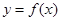 的单调增区间;
的单调增区间;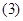 画出函数
画出函数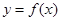 在区间
在区间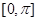 上的图象.
上的图象.
已知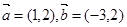 ,当
,当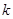 为何值时,
为何值时,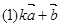 与
与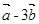 垂直?
垂直?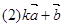 与
与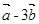 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?