某观测站C在A城的南偏西20°的方向.由A城出发的一条公路,走向是南偏东40°,在C处测得公路上B处有一人距C为31千米正沿公路向A城走去,走了20千米后到达D处,此时CD间的距离为21千米,问这人还要走多少千米才能到达A城?
计算以下式子的值:
(1) ;
;
(2)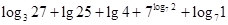 .
.
已知函数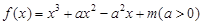 .
.
若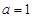 时函数
时函数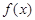 有三个互不相同的零点,求实数
有三个互不相同的零点,求实数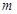 的取值范围;
的取值范围;
若对任意的 ,不等式
,不等式 对任意
对任意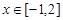 恒成立,求实数
恒成立,求实数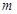 的取值范围.
的取值范围.
已知椭圆C的中心在原点,焦点在坐标轴上,短轴的一个端点B(0,4),离心率e=0.6.
(1)求椭圆C的方程;
(2)若O(0,0),P(2,2),试探究在椭圆C内部是否存在整点Q(平面内横、纵坐标都是
整数的点为整点),使得△OPQ的面积S△OPQ=4?若存在,请指出共有几个这样的点(不必具体求出这些点的坐标);否则,说明理由.
已知等比数列{ }的前
}的前 项和为
项和为 ,且满足
,且满足 .
.
(1)求 的值及数列{
的值及数列{ }的通项公式;
}的通项公式;
(2)若数列{ }满足
}满足 ,求数列{
,求数列{ }的前
}的前 和
和 .
.
已知 图象过点
图象过点 ,且在
,且在 处的切线方程是
处的切线方程是 .
.
(1)求 的解析式;
的解析式;
(2)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.