设a=(-1,1),b=(4,3),c=(5,-2),
(1)求证a与b不共线,并求a与b的夹角的余弦值;
(2)求c在a方向上的投影;
(3)求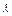 1和
1和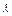 2,使c=
2,使c=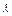 1a+
1a+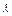 2b.
2b.
(本小题满分12分)如图,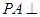 平面
平面 ,四边形
,四边形 是正方形,
是正方形,  ,点
,点 、
、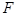 、
、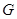 分别为线段
分别为线段 、
、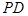 和
和 的中点.
的中点.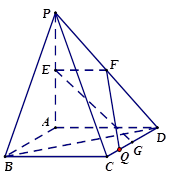
(Ⅰ)求异面直线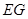 与
与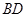 所成角的余弦值;
所成角的余弦值;
(Ⅱ)在线段 上是否存在一点
上是否存在一点 ,使得点
,使得点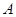 到平面
到平面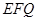 的距离恰为
的距离恰为 ?若存在,求出线段
?若存在,求出线段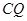 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
(本小题满分10分) 当 时,
时, ,
, .
.
(Ⅰ)求 ,
,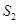 ,
, ,
,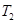 ;
;
(Ⅱ)猜想 与
与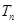 的大小关系,并用数学归纳法证明.
的大小关系,并用数学归纳法证明.
(本小题满分15分)
已知函数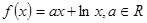
(Ⅰ)求函数 的极值;
的极值;
(Ⅱ)对于曲线上的不同两点 ,如果存在曲线上的点
,如果存在曲线上的点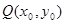 ,且
,且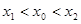 ,使得曲线在点
,使得曲线在点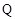 处的切线
处的切线 ∥
∥ ,则称
,则称 为弦
为弦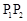 的伴随切线。特别地,当
的伴随切线。特别地,当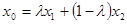 ,
,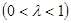 时,又称
时,又称 为
为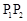 的λ——伴随切线。
的λ——伴随切线。
(ⅰ)求证:曲线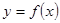 的任意一条弦均有伴随切线,并且伴随切线是唯一的;
的任意一条弦均有伴随切线,并且伴随切线是唯一的;
(ⅱ)是否存在曲线C,使得曲线C的任意一条弦均有 伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
伴随切线?若存在,给出一条这样的曲线 ,并证明你的结论; 若不存在 ,说明理由。
(本题满分15分)
已知各项均为正数的数列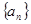 中,数列的前
中,数列的前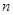 项和
项和 满足
满足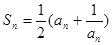 .
.
(1)求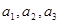 ;
;
(2)由(1)猜想数列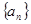 的通项公式,并用数学归纳法证明你的猜想.
的通项公式,并用数学归纳法证明你的猜想.
(本题满分14分)
一个口袋内有4个不同的红球,6个不同的白球.
(1)从中任取4个球,红球的个数不比白球少的取法有多少种?
(2)若取一个红球记2分,取一个白球记1分,从中任取4个球,使总分不少于7分的取法有多少种?