(本小题满分14分)已知函数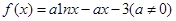 .
.
(1)讨论函数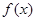 的单调性;
的单调性;
(2)若函数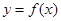 的图像在点
的图像在点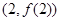 处的切线的倾斜角为45°,那么实数
处的切线的倾斜角为45°,那么实数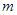 在什么范围取值时,函数
在什么范围取值时,函数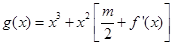 在区间(2,3)内总存在极值?
在区间(2,3)内总存在极值?
(3)求证: .
.
(本小题满分13分)某沿海地区养殖的一种特色海鲜上市时间仅能持续5个月,预测上市初期和厢期会因供应不足使价格呈
持续上涨态势,而中期又将出现供大于求使价格连续下跌.现有三种价格模拟函数:①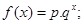 ②
② ③
③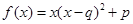 (以上三式中
(以上三式中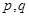 均为常数,且q>l).
均为常数,且q>l).
(1)为准确研究其价格走势,应选哪种价格模拟函数(不必说明理由);
(2)若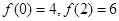 ,求出所选函数
,求出所选函数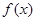 的解析式(注:函数定义域是
的解析式(注:函数定义域是 .其中
.其中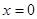 表示8
表示8
月1日,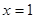 表示9月1日,…,以此类推);
表示9月1日,…,以此类推);
(3)在(2)的条件下研究下面课题:为保证养殖户的经济效益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该海鲜将在哪几个月份内价格下跌.
(本小题满分l3分)某大学志愿者协会有6窑男同学,4名女同学,在这10名同学中,3名同学自数学学院,其余7名同学
自物理、化学等其他互不相同的7个学院,现从这10名同学中随机选取3名同学,到希望小学进行支教活
动(每位同学被选到的可能性相同).
(1)求选出的3名同学是自互不相同学院的概率:
(2)设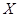 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量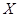 的分布列和数学期望.
的分布列和数学期望.
(本小题满分13分)设函数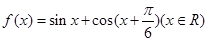
(1)求函数 的最小正周期及其在区间
的最小正周期及其在区间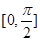 上的值域;
上的值域;
(2)记△ABC内角A,B,C的对边分别为a,b,c,若,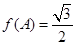 ,且
,且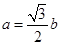 ,求角B的值.
,求角B的值.
(本小题满分13分)已知函数簇 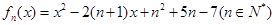 .
.
(1)设曲线列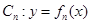 的顶点的纵坐标构成数列
的顶点的纵坐标构成数列 ,求证:数列
,求证:数列 为等差数列;
为等差数列;
(2)设曲线列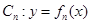 的顶点到
的顶点到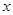 轴的距离构成数列
轴的距离构成数列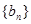 ,
, 为数列
为数列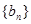 的前
的前 项和,求S20.
项和,求S20.