在海岸A处,发现北偏东45°方向,距离A( -1)n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2 n mile的C处的缉私船奉命以10
-1)n mile的B处有一艘走私船,在A处北偏西75°的方向,距离A 2 n mile的C处的缉私船奉命以10 n mile/h的速度追截走私船.此时,走私船正以10 n mile/h的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?
n mile/h的速度追截走私船.此时,走私船正以10 n mile/h的速度从B处向北偏东30°方向逃窜,问缉私船沿什么方向能最快追上走私船?
设向量 .
.
(Ⅰ)求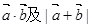 ;
;
(Ⅱ)若函数 ,求
,求 的最小值、最大值.
的最小值、最大值.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、
PC的中点.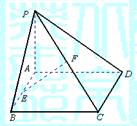
(1)求证:EF∥平面PAD;
(2)求证:EF⊥CD;
(3)若ÐPDA=45°求EF与平面ABCD所成的角的大小.
设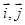 是直角坐标系中,x轴、y轴正方向上的单位向量,设
是直角坐标系中,x轴、y轴正方向上的单位向量,设
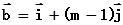
(1)若(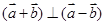 ,求
,求 .
.
(2)若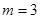 时,求
时,求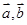 的夹角
的夹角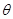 的余弦值.
的余弦值.
(3)是否存在实数 ,使
,使 ,若存在求出
,若存在求出 的值,不存在说明理由.
的值,不存在说明理由.
已知 ,求下列各式的值:
,求下列各式的值:
(1)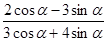
(2)
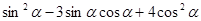
已知直线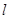 :y="k" (x+2
:y="k" (x+2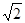 )与圆O:
)与圆O: 相交于A、B两点,O是坐标原点,
相交于A、B两点,O是坐标原点,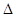 ABO的面积为S.
ABO的面积为S.
(1)试将S表示成的函数S(k),并求出它的定义域;
(2)求S的最大值,并求取得最大值时k的值.