(本小题满分12分)已知函数 ,
,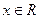
(1)求函数 的最大值及对应的
的最大值及对应的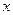 的取值集合;
的取值集合;
(2)在给定的坐标系中,画出函数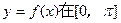 上的图象。
上的图象。
(本小题满分12分)已知数列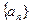 是等差数列,
是等差数列,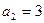 ,
, ,
, 为数列
为数列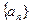 的前
的前 项和
项和
(1)求 和
和 ;(2)若
;(2)若 ,求数列
,求数列 的前
的前 项和
项和
(本小题满分14分)
已知数列 是首项为
是首项为 ,公差为
,公差为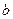 的等差数列,
的等差数列, 是首项为
是首项为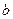 ,公比为
,公比为 的等比数列,且满足
的等比数列,且满足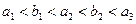 ,其中
,其中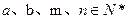 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若数列 与数列
与数列 有公共项,将所有公共项按原顺序排列后构成一个新数列
有公共项,将所有公共项按原顺序排列后构成一个新数列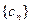 ,求数列
,求数列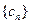 的通项公式;
的通项公式;
(Ⅲ)记(Ⅱ)中数列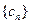 的前项之和为
的前项之和为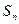 ,求证:
,求证: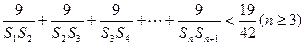
((本小题满分14分)
设椭圆 的左右焦点分别为
的左右焦点分别为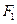 、
、 ,
, 是椭圆
是椭圆 上的一点,
上的一点, ,坐标原点
,坐标原点 到直线
到直线 的距离为
的距离为 .
.
(1)求椭圆 的方程;
的方程;
(2)设 是椭圆
是椭圆 上的一点,过点
上的一点,过点 的直线
的直线 交
交 轴于点
轴于点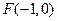 ,交
,交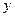 轴于点
轴于点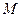 ,若
,若 ,求直线
,求直线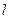 的斜率.
的斜率.
(本小题满分14分)
设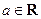 ,函数
,函数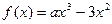 .
.
(Ⅰ)若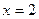 是函数
是函数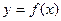 的极值点,求实数
的极值点,求实数 的值;
的值;
(Ⅱ)若函数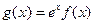 在
在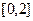 上是单调减函数,求实数
上是单调减函数,求实数 的取值范围.
的取值范围.