如图所示,P是抛物线C:y= x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q,当点P在抛物线C上移动时,求线段PQ的中点M的轨迹方程,并求点M到x轴的最短距离.
x2上一点,直线l过点P并与抛物线C在点P的切线垂直,l与抛物线C相交于另一点Q,当点P在抛物线C上移动时,求线段PQ的中点M的轨迹方程,并求点M到x轴的最短距离.
已知点是F抛物线 与椭圆
与椭圆 的公共焦点,且椭圆的离心率为
的公共焦点,且椭圆的离心率为

(1)求椭圆的方程;
(2)过抛物线上一点P,作抛物线的切线 ,切点P在第一象限,如图,设切线
,切点P在第一象限,如图,设切线 与椭圆相交于不同的两点A、B,记直线OP,FA,FB的斜率分别为
与椭圆相交于不同的两点A、B,记直线OP,FA,FB的斜率分别为 (其中
(其中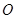 为坐标原点),若
为坐标原点),若 ,求点P的坐标.
,求点P的坐标.
已知函数 .
.
(1)求: 的值;
的值;
(2)类比等差数列的前 项和公式的推导方法,求:
项和公式的推导方法,求: 的值.
的值.
请观察以下三个式子:
①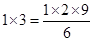 ;
;
②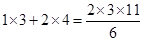 ;
;
③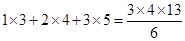 ,
,
归纳出一般的结论,并用数学归纳法证明之.
已知复数 ,且
,且 ,若
,若 在复平面中对应的点分别为
在复平面中对应的点分别为 ,求
,求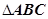 的面积.
的面积.
设函数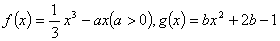 .
.
(I)若曲线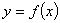 与曲线
与曲线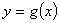 在它们的交点
在它们的交点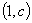 处具有公共切线,求
处具有公共切线,求 的值;
的值;
(II)当 时,若函数
时,若函数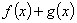 在区间
在区间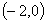 内恰有两个零点,求
内恰有两个零点,求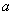 的取值范围;
的取值范围;
(III)当 时,求函数
时,求函数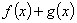 在区间
在区间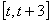 上的最大值
上的最大值