用数学归纳法证明不等式: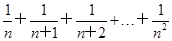 >1(n∈N*且n>1).
>1(n∈N*且n>1).
设数列{an}的前n项和为Sn.已知a1=1, =an+1-
=an+1-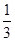 n2-n-
n2-n-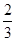 ,n∈N*.
,n∈N*.
(1)求a2的值;
(2)求数列{an}的通项公式;
(3)证明:对一切正整数n,有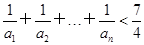 .
.
已知f(n)=1+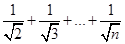 n∈N),g(n)=2(
n∈N),g(n)=2(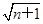 -1)(n∈N).
-1)(n∈N).
(1)当n=1,2,3时,分别比较f(n)与g(n)的大小(直接给出结论);
(2)由(1)猜想f(n)与g(n)的大小关系,并证明你的结论.
已知数列{an}满足a1=1,且4an+1-anan+1+2an=9(n∈N).
(1)求a2,a3,a4的值;
(2)由(1)猜想{an}的通项公式,并给出证明.
已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=145.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=loga (其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与
(其中a>0且a≠1).记Sn是数列{an}的前n项和,试比较Sn与 logabn+1的大小,并证明你的结论.
logabn+1的大小,并证明你的结论.