圆C与y轴相切,圆心在射线 x-3y=0(x>0)上,且圆C截直线y=x所得弦长为 . (1)求圆C的方程。(2)点P(x,y)是圆C上的动点,求x+y的最大值。(3)求过点M(2,1)的圆的弦的中点轨迹方程。
. (1)求圆C的方程。(2)点P(x,y)是圆C上的动点,求x+y的最大值。(3)求过点M(2,1)的圆的弦的中点轨迹方程。
设函数 ,其中
,其中 。
。
(1)当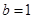 时,
时,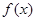 在
在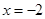 时取得极值,求
时取得极值,求 ;
;
(2)当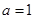 时,若
时,若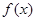 在
在 上单调递增,求
上单调递增,求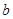 的取值范围;
的取值范围;
(3)证明对任意的正整数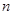 ,不等式
,不等式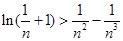 都成立。
都成立。
已知椭圆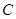 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 轴上,离心率为
轴上,离心率为 ,椭圆的短轴端点和焦点所组成的四边形周长等于8。
,椭圆的短轴端点和焦点所组成的四边形周长等于8。
(Ⅰ)求椭圆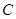 的方程;
的方程;
(Ⅱ)若过点 的直线
的直线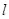 与椭圆
与椭圆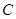 相交于
相交于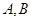 两点(
两点( 不是左右顶点),且以
不是左右顶点),且以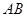 为直径的圆过椭圆
为直径的圆过椭圆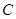 的右顶点,求直线
的右顶点,求直线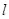 的方程。
的方程。
已知数列 满足:
满足: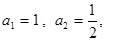 且
且 .
.
(Ⅰ)求 ,
, ,
, ,
, 的值及数列
的值及数列 的通项公式;
的通项公式;
(Ⅱ)设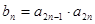 ,求数列
,求数列 的前
的前 项和
项和 ;
;
已知斜三棱柱 ,
, ,
,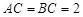 ,
, 在底面
在底面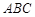 上的射影恰为
上的射影恰为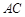 的中点
的中点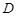 ,又知
,又知 .
.
(Ⅰ)求证: 平面
平面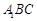 ;
;
(Ⅱ)求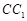 到平面
到平面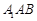 的距离;
的距离;
(Ⅲ)求二面角 的大小。
的大小。
某车站每天上午发出两班客车,第一班客车在8∶00,8∶20,8∶40这三个时刻随机发出,且在8∶00发出的概率为 ,8∶20发出的概率为
,8∶20发出的概率为 ,8∶40发出的概率为
,8∶40发出的概率为 ;第二班客车在9∶00,9∶20,9∶40这三个时刻随机发出,且在9∶00发出的概率为
;第二班客车在9∶00,9∶20,9∶40这三个时刻随机发出,且在9∶00发出的概率为 ,9∶20发出的概率为
,9∶20发出的概率为 ,9∶40发出的概率为
,9∶40发出的概率为  .两班客车发出时刻是相互独立的,一位旅客预计8∶10到站.求:
.两班客车发出时刻是相互独立的,一位旅客预计8∶10到站.求:
(1)请预测旅客乘到第一班客车的概率;
(2)旅客候车时间的分布列;
(3)旅客候车时间的数学期望。