已知数列{an}和{bn}满足：a1=
,an+1=
an+n-4,bn=(-1)n(an-3n+21),其中为实数，n为正整数.
（1）证明：对任意实数,数列{an}不是等比数列；
（2）证明：当≠-18时，数列{bn}是等比数列；
（3）设Sn为数列{bn}的前n项和.是否存在实数,使得对任意正整数n，都有Sn＞-12?若存在，求的取值范围；若不存在，说明理由.
（本小题满分10分）已知直线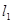
为曲线
在点
处的切线，
为该曲线的另一条切线，且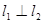
.
求：（1）求直线的方程；（2）求由直线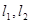
和
轴所围成的三角形的面积.
（本小题满分10分）已知函数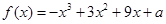
(
)
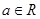（1）求函数
的极大值和极小值；
（2）若函数在区间[－2，2]上的最大值为20，求它在该区间上的最小值。
（本小题满分10分）袋中有4个红球，3个黑球，从袋中随机取球，设取到一个红球得2分，取到一个黑球的1分，现在从袋中随机摸出4个球，
求：（1）列出所得分数X的分布列；（2）得分大于6分的概率。
、（本小题满分9分）已知函数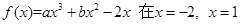
处取得极值。（1）求函数
的解析式；
（2）求函数的单调区间
（本小题满分14分） 若椭圆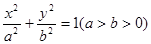
过点
，离心率为
，⊙O的圆心在原点，直径为椭圆的短轴，⊙M的方程为
，过⊙M上任一点P作⊙O的切线PA、PB，切点为A、B.
(1) 求椭圆的方程；
（2）若直线PA与⊙M的另一交点为Q，当弦PQ最大时，求直线PA的方程。