函数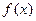 是定义在
是定义在 上的偶函数,当
上的偶函数,当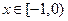 时,
时,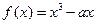 。
。
(1)当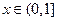 时,求
时,求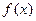 的解析式;
的解析式;
(2)若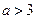 ,试判断
,试判断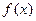 在
在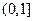 的单调性,并证明你的结论。
的单调性,并证明你的结论。
如图,AB是⊙O的直径,BE为⊙O的切线,点C为⊙O上不同于A,B的一点,AD为∠BAC的平分线,且分别与BC交于H,与⊙O交于D,与BE交于E,连接BD,CD.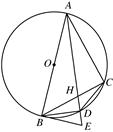
(1)求证:BD平分∠CBE;
(2)求证:AH·BH=AE·HC.
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.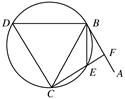
(1)证明:DB=DC;
(2)设圆的半径为1,BC=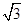 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明: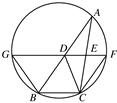
(1)CD=BC;
(2)△BCD∽△GBD.
如图,在正△ABC中,点D,E分别在边BC,AC上,且BD= BC,CE=
BC,CE= CA,AD,BE相交于点P,求证:
CA,AD,BE相交于点P,求证: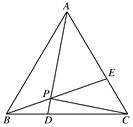
(1)P,D,C,E四点共圆;
(2)AP⊥CP.
在极坐标系中,O为极点,半径为2的圆C的圆心的极坐标为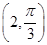 .
.
(1)求圆C的极坐标方程;
(2)P是圆C上一动点,点Q满足3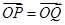 ,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.
,以极点O为原点,以极轴为x轴正半轴建立直角坐标系,求点Q的轨迹的直角坐标方程.