已知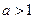 ,在函数
,在函数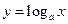
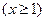 的图象上有
的图象上有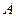 、
、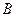 、
、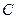 三点,它们的横坐标分别为
三点,它们的横坐标分别为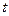 、
、 、
、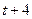 。
。
(1)若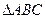 的面积为
的面积为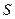 ,求
,求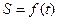 ;
;
(2)判断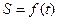 的单调性。
的单调性。
(本小题满分10分)某班组织的数学文化节活动中,通过抽奖产生了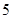 名幸运之星.这
名幸运之星.这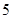 名幸运之星可获得
名幸运之星可获得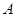 、
、 两种奖品中的一种,并规定:每个人通过抛掷一枚质地均匀的骰子决定自己最终获得哪一种奖品,抛掷点数小于
两种奖品中的一种,并规定:每个人通过抛掷一枚质地均匀的骰子决定自己最终获得哪一种奖品,抛掷点数小于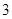 的获得
的获得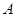 奖品,抛掷点数不小于
奖品,抛掷点数不小于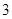 的获得
的获得 奖品.
奖品.
(1)求这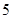 名幸运之星中获得
名幸运之星中获得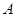 奖品的人数大于获得
奖品的人数大于获得 奖品的人数的概率;
奖品的人数的概率;
(2)设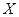 、
、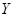 分别为获得
分别为获得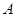 、
、 两种奖品的人数,并记
两种奖品的人数,并记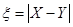 ,求随机变量
,求随机变量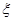 的分布列及数学期望.
的分布列及数学期望.
(本小题满分10分,不等式选讲)
已知不等式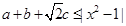 对于满足条件
对于满足条件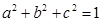 的任意实数
的任意实数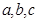 恒成立,求实数
恒成立,求实数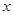 的取值范围.
的取值范围.
(本小题满分10分,坐标系与参数方程选讲)
已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的正半轴重合.若直线l的极坐标方程为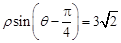 .
.
(1)把直线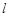 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)已知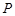 为椭圆
为椭圆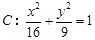 上一点,求
上一点,求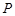 到直线
到直线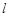 的距离的最小值.
的距离的最小值.
(本小题满分10分,矩阵与变换)
已知矩阵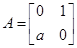 ,矩阵
,矩阵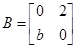 ,直线
,直线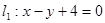 经矩阵
经矩阵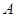 所对应的变换得到直线
所对应的变换得到直线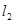 ,直线
,直线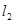 又经矩阵
又经矩阵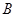 所对应的变换得到直线
所对应的变换得到直线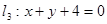 .
.
(1)求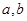 的值;(2)求直线
的值;(2)求直线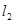 的方程.
的方程.
(本小题满分10分,几何证明选讲)
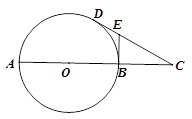
如图,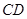 是圆
是圆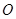 的切线,切点为
的切线,切点为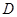 ,
,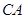 是过圆心的割线且交圆
是过圆心的割线且交圆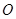 于
于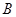 点,过
点,过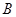 作
作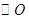 的切线交
的切线交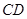 于点
于点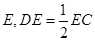 .
.
求证:(1)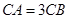 ;(2)
;(2)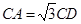 .
.