一项“过关游戏”规则规定:在第n关要抛掷一颗骰子n次,如果这n次抛掷所出现的点数之和大于 ,则算过关。问:(Ⅰ)某人在这项游戏中最多能过几关?(Ⅱ)他连过前三关的概率是多少?(注:骰子是一个在各面上分别有1,2,3,4,5,6点数的均匀正方体。抛掷骰子落地静止后,向上一面的点数为出现点数。)
,则算过关。问:(Ⅰ)某人在这项游戏中最多能过几关?(Ⅱ)他连过前三关的概率是多少?(注:骰子是一个在各面上分别有1,2,3,4,5,6点数的均匀正方体。抛掷骰子落地静止后,向上一面的点数为出现点数。)
设数列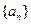 的前n项和为
的前n项和为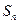 ,且
,且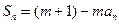 对任意正整数n都成立,其中
对任意正整数n都成立,其中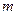 为常数,且
为常数,且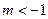 ,(1)求证:
,(1)求证: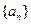 是等比数列;(2)设数列
是等比数列;(2)设数列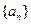 的公比
的公比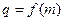 ,数列
,数列 满足:
满足: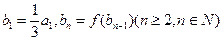 ,求数列
,求数列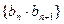 的前
的前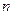 项和
项和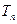 。
。
(本小题满分12分)
如图甲,在平面四边形ABCD中,已知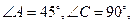
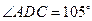 ,
,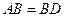 ,现将四边形ABCD沿BD折起,使平面ABD
,现将四边形ABCD沿BD折起,使平面ABD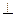 平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.
平面BDC(如图乙),设点E、F分别为棱AC、AD的中点.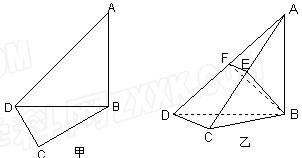
(1)求证:DC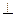 平面ABC;
平面ABC;
(2)设 ,求三棱锥A-BFE的体积.
,求三棱锥A-BFE的体积.
在△ABC中,角A、B、C的对边分别为a、b、c,若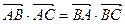
(1)判断△ABC的形状
(2)若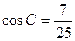 ,求
,求 的值
的值
(本小题满分14分)
数列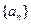 的前n项和为
的前n项和为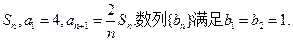

(I)求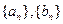 的通项公式;
的通项公式;
(II)求证: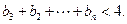
(本小题共12分)
已知函数 的导函数为
的导函数为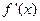 ,且不等式
,且不等式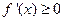 的解集
的解集
为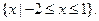
(I)若函数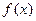 的极大值为0,求实数a的值;
的极大值为0,求实数a的值;
(II)当x满足不等式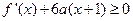 时,关于x的方程
时,关于x的方程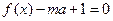 有唯一实数解,求实数m的取值范围。
有唯一实数解,求实数m的取值范围。