在函数 ,
, 的图象中,试指出曲线的位置,对称轴、渐近线以及函数的奇偶性、单调性和最大值分别是什么;指出参数
的图象中,试指出曲线的位置,对称轴、渐近线以及函数的奇偶性、单调性和最大值分别是什么;指出参数 与曲线形状的关系,并运用指数函数的有关性质加以说明.
与曲线形状的关系,并运用指数函数的有关性质加以说明.
如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去
四个相同的小正方形,制成一个无盖的小盒子,问小正方形的
边长为多少时,盒子容积最大?
已知曲线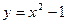 与
与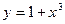 在
在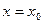 处的切线互相垂直,求
处的切线互相垂直,求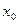 的值
的值
(本小题满分14分)
椭圆 与直线
与直线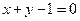 相交于两点
相交于两点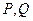 ,且
,且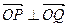
(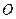 为原点).
为原点).
(1)求证: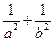 为定值;(2)若离心率
为定值;(2)若离心率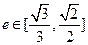 ,求椭圆长轴的取值范围。
,求椭圆长轴的取值范围。
(本小题满分12分)
已知抛物线以原点为顶点,以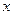 轴为对称轴,焦点在直线
轴为对称轴,焦点在直线 上.
上.
(1)求抛物线的方程;(2)设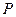 是抛物线上一点,点
是抛物线上一点,点 的坐标为
的坐标为 ,求
,求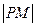 的最小值(用
的最小值(用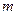 表示),并指出此时点
表示),并指出此时点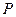 的坐标。
的坐标。
(本小题满分12分)
已知两点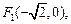
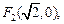 满足条件
满足条件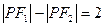 的动点P的轨迹是曲线E,直线l:y= kx-1与曲线E交于A、B两个不同点。
的动点P的轨迹是曲线E,直线l:y= kx-1与曲线E交于A、B两个不同点。
(1)求k的取值范围;(2)如果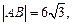 求直线l的方程.
求直线l的方程.