假设一个人从出生到死亡,在每个生日都测量身高,并作出这些数据散点图,则这些点将不会落在一条直线上,但在一段时间内的增长数据有时可以用线性回归来分析.下表是一位母亲给儿子作的成长记录:
| 年龄/周岁 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 身高/cm |
90.8 |
97.6 |
104.2 |
110.9 |
115.6 |
122.0 |
128.5 |
| 年龄/周岁 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| 身高/cm |
134.2 |
140.8 |
147.6 |
154.2 |
160.9 |
167.6 |
173.0 |
(1)作出这些数据的散点图;
(2)求出这些数据的回归方程;
(3)对于这个例子,你如何解释回归系数的含义?
(4)用下一年的身高减去当年的身高,计算他每年身高的增长数,并计算他从3~16岁身高的年均增长数.
(5)解释一下回归系数与每年平均增长的身高之间的联系.
(本题12分).如图,四棱柱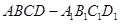 中,侧棱
中,侧棱 ⊥底面ABCD,AB//DC,AB⊥AD,AD=CD=1,
⊥底面ABCD,AB//DC,AB⊥AD,AD=CD=1, =AB=2,E为棱
=AB=2,E为棱 的中点.
的中点.
(Ⅰ)证明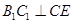
(Ⅱ)求二面角 的正弦值.
的正弦值.
(Ⅲ)设点M在线段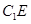 上,且直线AM与平面
上,且直线AM与平面 所成角的正弦值为
所成角的正弦值为 ,求线段AM的长.
,求线段AM的长.
(本题12分)如图,在三棱锥A-BOC中,OA⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,BC=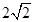 ,动点D在线段AB上.
,动点D在线段AB上.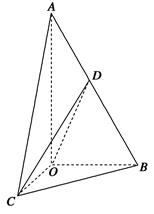
(1)求证:平面COD⊥平面AOB;
(2)当OD⊥AB时,求三棱锥C-OBD的体积.
(本题12分)如图,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AP=AB,BP=BC=2,E,F分别是PB,PC的中点.
(Ⅰ)证明:EF∥平面PAD;
(Ⅱ)求四棱锥P—ABCD的表面积S.
(本题12分) 的内角
的内角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
,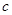 .向量
.向量 与
与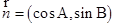 平行.
平行.
(Ⅰ)求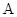 ;
;
(Ⅱ)若 ,
, ,求
,求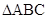 的面积.
的面积.
(本题10分)已知不等式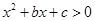 的解集为
的解集为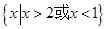 .
.
(1)求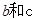 的值;
的值;
(2)求不等式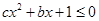 的解集
的解集