已知数列{an}中,a1=2,n∈N*,an>0,数列{an}的前n项和为Sn,且满足an+1= .
.
(1)求{Sn}的通项公式;
(2)设{bk}是{Sn}中的按从小到大顺序组成的整数数列.
①求b3;
②存在N(N∈N*),当n≤N时,使得在{Sn}中,数列{bk}有且只有20项,求N的范围.
如图,在四棱台ABCD-A1B1C1D1中,DD1 平面ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,
平面ABCD,底面ABCD是平行四边形,AB=AD=2A1B1,

(1)证明:BB1 AC;
AC;
(2)若AB=2,且二面角A1-AB-C大小为60 ,连接AC,BD,设交点为O,连接B1O。求三棱锥B1-ABO外接球的体积。(球体体积公式:
,连接AC,BD,设交点为O,连接B1O。求三棱锥B1-ABO外接球的体积。(球体体积公式: ,R是球半径)
,R是球半径)
已知数列 各项都是正数,且
各项都是正数,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)令 ,
, ,求数列
,求数列 的前
的前 项和
项和 .
.
在某次考试中,从甲乙两个班各抽取10名学生的数学成绩进行统计分析,两个班成绩的茎叶图如图所示,成绩不小于90分的为及格。

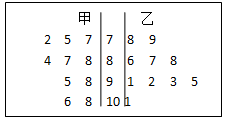
(1)用样本估计总体,请根据茎叶图对甲乙两个班级的成绩进行比较。
(2)在甲乙两班的成绩及格的同学中在随机抽取两名同学的试卷做分析,求抽出的两人恰好都是甲班学生的概率.
(本小题满分10分)选修4-5:不等式选讲
已知函数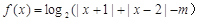 .
.
(1)当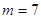 时,求函数
时,求函数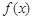 的定义域;
的定义域;
(2)若关于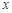 的不等式
的不等式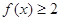 的解集是
的解集是 ,求
,求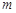 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,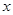 轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度. 已知曲线
轴的正半轴为极轴建立极坐标系,两种坐标系取相同的单位长度. 已知曲线
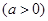 ,过点
,过点 的直线
的直线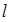 的参数方程为
的参数方程为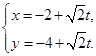 (t为参数)。直线
(t为参数)。直线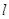 与曲线
与曲线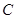 分别交于
分别交于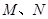 .若
.若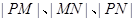 成等比数列,求实数
成等比数列,求实数 的值。
的值。