某学生计算一离散型随机变量X的分布列如表：
 |
 |
0 |
1 |
2 |
 |
 |
 |
|
|
试说明该学生的计算是否正确；如果不正确，请说明理由．
（本小题满分12分）
设锐角三角形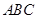
的内角
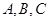的对边分别为
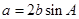
（I）求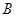
的大小；
（II）若
，
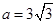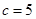，求
．
（本小题满分12分）
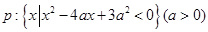设命题
,命题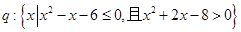
(1)如果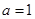
，且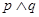
为真时，求实数
的取值范围；
(2)若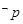
是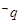
的充分不必要条件时，求实数
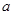的取值范围.
（本小题满分12分） 已知函数
，
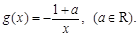
（1）设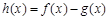函数
，求函数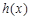
的单调区间；
（2）若在区间
（
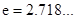）上存在一点
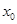，使得
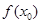
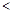
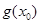成立，求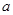
的取值范围.
（本小题满分12分）
设数列
对任意正整数n都成立，m为大于—1的非零常数。
（1）求证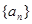
是等比数列；
（2设数列
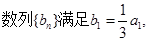
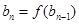
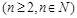
求证：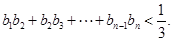
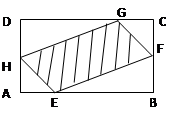
如图，有一块矩形空地，要在这块空地上辟一个内接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知AB＝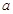
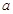（>2），BC＝2，且AE＝AH＝CF＝CG，设AE＝
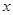，绿地面积为
.
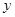（1）写出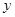关于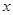的函数关系式，并指出这个函数的定义域;
（2）当AE为何值时，绿地面积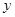最大？