一个口袋内装有5个小球,另一个口袋内装有4个小球,所有这些小球的颜色互不相同.
(1)从两个口袋内任取一个小球,有多少种不同的取法?
(2)从两个口袋内各取一个小球,有多少种不同的取法?
(本小题满分10分)选修4—5 不等式证明选讲
已知 是不相等的正实数,求证:
是不相等的正实数,求证: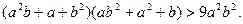
(本小题满分10分)选修4—4 参数方程与极坐标
求圆 被直线
被直线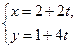 (
(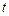 是参数
是参数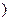 截得的弦长.
截得的弦长.
(本小题满分10分)选修4—1 几何证明选讲
在直径是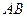 的半圆上有两点
的半圆上有两点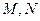 ,设
,设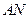 与
与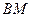 的交点是
的交点是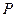 .求证:
.求证: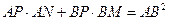
 |
(本小题满分12分)已知函数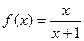 .
.
(Ⅰ)求函数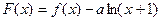 的单调递增区间;
的单调递增区间;
(Ⅱ)数列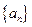 满足:
满足: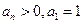 ,且
,且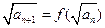 ,记数列
,记数列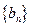 的前n项和为
的前n项和为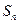 ,
,
且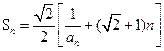 .
.
(ⅰ)求数列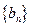 的通项公式;并判断
的通项公式;并判断 是否仍为数列
是否仍为数列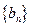 中的项?若是,请证明;否则,说明理由.
中的项?若是,请证明;否则,说明理由.
(ⅱ)设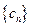 为首项是
为首项是 ,公差
,公差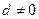 的等差数列,求证:“数列
的等差数列,求证:“数列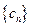 中任意不同两项之和仍为数列
中任意不同两项之和仍为数列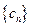 中的项”的充要条件是“存在整数
中的项”的充要条件是“存在整数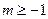 ,使
,使 ”
”
(本小题满分12分)
|
已知椭圆 :
: 的一个焦点是(1,0),两个焦点与短轴的一个端点
的一个焦点是(1,0),两个焦点与短轴的一个端点
 的方程;
的方程;
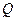 (4,0)且不与坐标轴垂直的直线
(4,0)且不与坐标轴垂直的直线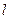 交椭圆
交椭圆 于
于 、
、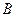 两点,设点
两点,设点 关于
关于 轴的对称点为
轴的对称点为 .
.
 过
过 轴上一定点,并求出此定点坐标;
轴上一定点,并求出此定点坐标;
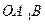 面积的取值范围.
面积的取值范围.