某圆拱桥的水面跨度20m,拱高4m。现有一船,宽10m,水面以上高3m,这条船能否从桥下通过?
(本小题满分14分)已知函数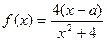 .
.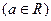 (Ⅰ)判断
(Ⅰ)判断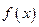 的奇偶性;(Ⅱ)设方程
的奇偶性;(Ⅱ)设方程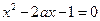 的两实根为
的两实根为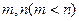 ,证明函数
,证明函数 是
是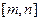 上的增函数.
上的增函数.
(本小题满分13分)某隧道长2150m,通过隧道的车速不能超过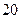 m/s.一列有55辆车身长都为10m的同一车型的车队(这种型号的车能行驶的最高速为40m/s),匀速通过该隧道,设车队的速度为
m/s.一列有55辆车身长都为10m的同一车型的车队(这种型号的车能行驶的最高速为40m/s),匀速通过该隧道,设车队的速度为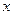 m/s ,根据安全和车流的需要,当
m/s ,根据安全和车流的需要,当 时,相邻两车之间保持20 m的距离;当
时,相邻两车之间保持20 m的距离;当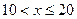 时,相邻两车之间保持
时,相邻两车之间保持 m的距离.自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为
m的距离.自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为 .(I)将
.(I)将 表示为
表示为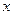 的
的 函数;(II)求车队通过隧道时间
函数;(II)求车队通过隧道时间 的最小值及此时车队的速度.
的最小值及此时车队的速度.
(本小题满分13分)设数列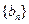 的前
的前 项和为
项和为 ,且
,且 ;数列
;数列 为等差数列,且
为等差数列,且
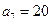 .
.
(Ⅰ)求数列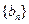 的通项公式;(Ⅱ)若
的通项公式;(Ⅱ)若 为数列
为数列 的前
的前 项和,求
项和,求 .
.
(本小题满分13分)设函数 .
. (Ⅰ)求函数
(Ⅰ)求函数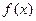 的单调区间;(Ⅱ)若常数
的单调区间;(Ⅱ)若常数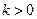 ,求不等式
,求不等式 的解集.
的解集.
(本小题满分13分)已知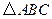 的角
的角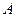 、
、 、
、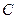 所对的边分别是
所对的边分别是 、
、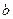 、
、 ,设向量
,设向量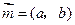 ,
,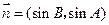 ,
, .(Ⅰ)若
.(Ⅰ)若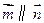 ,求证:
,求证: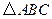 为等腰三角形;(Ⅱ)若
为等腰三角形;(Ⅱ)若 ,边长
,边长 ,角
,角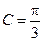 ,求
,求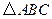 的面积
的面积 .
.