(本小题满分16分)已知⊙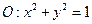 和点
和点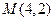 .
.

(Ⅰ)过点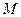 向⊙
向⊙ 引切线
引切线 ,求直线
,求直线 的方程;
的方程;
(Ⅱ)求以点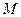 为圆心,且被直线
为圆心,且被直线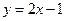 截得的弦长为 4的⊙
截得的弦长为 4的⊙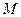 的方程;
的方程;
(Ⅲ)设 为(Ⅱ)中⊙
为(Ⅱ)中⊙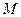 上任一点,过点
上任一点,过点 向⊙
向⊙ 引切线,切点为Q. 试探究:平面内是否存在一定点
引切线,切点为Q. 试探究:平面内是否存在一定点 ,使得
,使得 为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请举出一例,并指出相应的定值;若不存在,请说明理由.
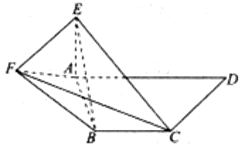
如图,在直角梯形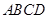 中,
中,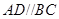 ,
,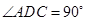 ,
,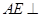 平面
平面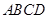 ,
,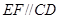 ,
,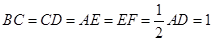 .
.
(Ⅰ)求证: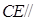 平面
平面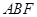 ;
;
(Ⅱ)在直线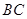 上是否存在点
上是否存在点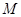 ,使二面角
,使二面角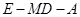 的大小为
的大小为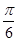 ?若存在,求出
?若存在,求出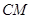 的长;若不存在,说明理由.
的长;若不存在,说明理由.
已知向量 .
.
(Ⅰ)若 ,求
,求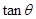 的值;
的值;
(Ⅱ)若 ,求
,求 的值.
的值.
选修4—5:《不等式选讲》
已知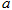 、
、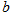 、c为正数.
、c为正数.
(1)若直线2x-(b-3)y+6=0与直线bx+ay-5=0互相垂直,试求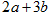 的最小值;
的最小值;
(2)求证: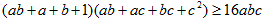 .
.
选修4-4:极坐标与参数方程
已知曲线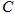 的参数方程是
的参数方程是 ,直线
,直线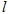 的参数方程为
的参数方程为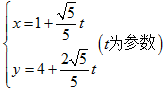 .
.
(1)求曲线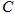 与直线
与直线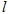 的普通方程;
的普通方程;
(2)若直线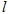 与曲线
与曲线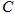 相交于
相交于 两点,且
两点,且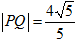 ,求实数
,求实数 的值.
的值.
选修4-1:几何证明选讲
如图,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,且EC=ED.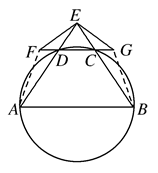
(1)证明:CD∥AB;
(2)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.