选修4-4:极坐标与参数方程
已知曲线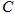 的参数方程是
的参数方程是 ,直线
,直线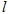 的参数方程为
的参数方程为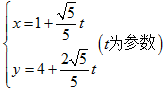 .
.
(1)求曲线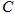 与直线
与直线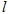 的普通方程;
的普通方程;
(2)若直线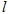 与曲线
与曲线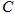 相交于
相交于 两点,且
两点,且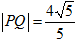 ,求实数
,求实数 的值.
的值.
(本小题满分12分)
已知点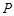 是圆
是圆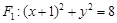 上任意一点,点
上任意一点,点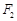 与点
与点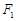 关于原点对称.线段
关于原点对称.线段 的中垂线
的中垂线 分别与
分别与 交于
交于 两点.
两点.
(1)求点 的轨迹
的轨迹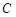 的方程;
的方程;
(2)斜率为1的直线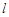 与曲线
与曲线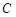 交于
交于 两点,若
两点,若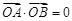 (
( 为坐标原点),求直线
为坐标原点),求直线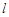 的方程.
的方程.
(本小题满分12分)
如图,在四棱锥S—ABCD中,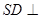 底面ABCD,底面ABCD是矩形,
底面ABCD,底面ABCD是矩形,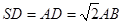 ,E是SA的中点.
,E是SA的中点.
(1)求证:平面BED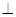 平面SAB;
平面SAB;
(2)求直线SA与平面BED所成角的大小.
(本小题满分14分)已知函数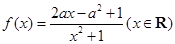 ,其中
,其中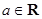 .
.
(Ⅰ)当 时,求曲线
时,求曲线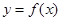 在点
在点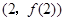 处的切线方程;
处的切线方程;
(Ⅱ)当 时,求函数
时,求函数 的单调区间与极值.
的单调区间与极值.
(本小题满分14分)已知圆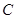 过点
过点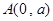
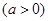 , 且在
, 且在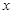 轴上截得的弦
轴上截得的弦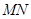 的长为
的长为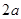 .
.
(1) 求圆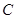 的圆心的轨迹方程;
的圆心的轨迹方程;
(2) 若 , 求圆
, 求圆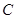 的方程.
的方程.
(本小题满分14分)设数列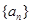 的前
的前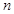 项和为
项和为 ,点
,点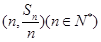 均在函数
均在函数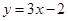 的图像上.
的图像上.
(Ⅰ)求数列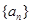 的通项公式;
的通项公式;
(Ⅱ)设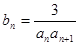 ,
, 是数列
是数列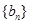 的前
的前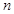 项和,求使得
项和,求使得 对所有
对所有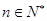 都成立的最小正整数
都成立的最小正整数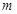 .
.