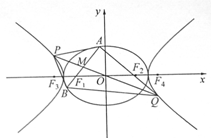
如图,为坐标原点,椭圆()的左右焦点分别为,离心率为;双曲线的左右焦点分别为,离心率为,已知,且.
(1)求的方程;
(2)过点作的不垂直于轴的弦,为的中点,当直线与交于两点时,求四边形面积的最小值.
(本小题满分14分)在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)由表中统计数据填写下边 列联表,并判断是否有
列联表,并判断是否有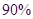 的把握认为“测评结果优秀与性别有关”.
的把握认为“测评结果优秀与性别有关”.
| 男生 |
女生 |
总计 |
|
| 优秀 |
|||
| 非优秀 |
|||
| 总计 |
参考数据与公式: ,其中
,其中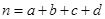 .
.
临界值表:
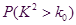 |
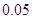 |
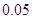 |
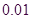 |
 |
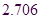 |
 |
 |
(本小题满分12分)如图ABCD是正方形,O是正方形的中心,PO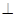 底面 ABCD,E是PC的中点.
底面 ABCD,E是PC的中点.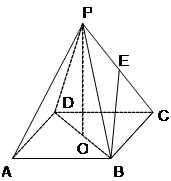
求证:(1)PA//平面BDE;(2)平面PAC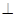 平面BDE.
平面BDE.
(本小题满分12分)已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 在区间
在区间 上的最小值和最大值.
上的最小值和最大值.
已知函数 ,
, (其中
(其中 ).
).
(Ⅰ)如果函数 和
和 有相同的极值点,求
有相同的极值点,求 的值,并直接写出函数
的值,并直接写出函数 的单调区间;
的单调区间;
(Ⅱ)求方程 在区间
在区间 上实数解的个数.
上实数解的个数.
已知两点 、
、 ,动点
,动点 与
与 、
、 两点连线的斜率
两点连线的斜率 、
、 满足
满足 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ) 是曲线
是曲线 与
与 轴正半轴的交点,曲线
轴正半轴的交点,曲线 上是否存在两点
上是否存在两点 、
、 ,使得
,使得 是以
是以 为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.
为直角顶点的等腰直角三角形?若存在,请说明有几个;若不存在,请说明理由.