如图,已知直四棱柱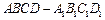 中,
中,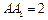 ,底面
,底面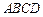 是直角梯形,
是直角梯形,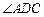 是直角,
是直角,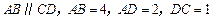 ,求异面直线
,求异面直线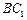 与
与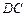 所成角的大小.
所成角的大小.
(1)计算:
(2)计算:
(本小题满分14分)若集合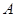 具有以下性质:
具有以下性质:
① ,
, ;
;
②若 ,则
,则 ,且
,且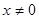 时,
时,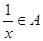 .
.
则称集合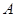 是“好集”.
是“好集”.
(Ⅰ)分别判断集合 ,有理数集
,有理数集 是否是“好集”,并说明理由;
是否是“好集”,并说明理由;
(Ⅱ)设集合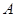 是“好集”,求证:若
是“好集”,求证:若 ,则
,则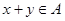 ;
;
(Ⅲ)对任意的一个“好集”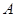 ,
, 分别判断下面命题的真假,并说明理由.
分别判断下面命题的真假,并说明理由.
命题 :若
:若 ,则必有
,则必有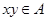 ;
;
命题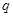 :若
:若
 ,且
,且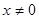 ,则必有
,则必有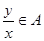 ;
;
(本小题满分13分)已知椭圆 :
: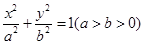 的右焦点为
的右焦点为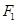
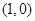 ,离心率为
,离心率为 .
.
(Ⅰ)求椭圆 的方程及左顶点
的方程及左顶点 的坐标;
的坐标;
(Ⅱ)设过点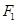 的直线交椭圆
的直线交椭圆 于
于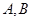 两点,若
两点,若 的面积为
的面积为 ,求直线
,求直线 的方程.
的方程.
(本小题满分13分)已知函数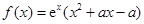 ,其中
,其中 是常数.
是常数.
(Ⅰ)当 时,求
时,求 在点
在点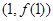 处的切线方程;
处的切线方程;
(Ⅱ)求 在区间
在区间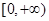 上的最小值.
上的最小值.
(本小题满分13分)在四棱锥 中,底面
中,底面 是菱形,
是菱形, .
.
(Ⅰ)若 ,求证:
,求证: 平面
平面 ;
;
(Ⅱ)若平面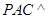 平
平 面
面 ,求证:
,求证: ;
;
(Ⅲ)在棱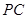 上是否存在点
上是否存在点 (异于点
(异于点 )使得
)使得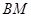 ∥平面
∥平面 ,若存在,求
,若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.