经调查某校高三年级学生家庭月平均收入不多于10000元的共有1000人，统计这些学生家庭月平均收入情况，得到家庭月平均收入频率分布直方图如图所示．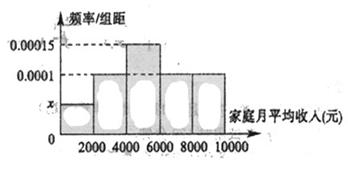
某企业准备给该校高三学生发放助学金，发放规定为：家庭收入在4000元以下（≤4000元）的每位同学得助学金2000元，家庭收入在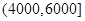
(元)间的每位同学得助学金1500元，家庭收入在
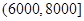(元)间的每位同学得助学金1000元，家庭收入在
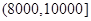(元)间的同学不发助学金．
(1)求频率分布直方图中的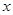
值；
(2)求该校高三年级学生中获得1500元助学金以上（≥1500元）的人数．
如图,在四棱椎P－ABCD中,底面ABCD是边长为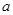
的正方形,且PD=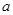,PA=PC=
.
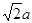(1)求证:直线PD⊥面ABCD;
(2)求二面角A－PB－D的大小.
等比数列{an}的前n项的和为Sn，已知S1，S3，S2成等差数列.
（1）求{an}的公比q；
（2）若a1-a3=3,求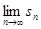
.
（1）在10000张有奖储蓄的奖券中，设有1个一等奖，5个二等奖，10个三等奖，从中买一张奖券，求中奖的概率；
（2）一批产品共10件，其中有两件次品，现随机地抽取5件，求所取5件中至多有一件次品的概率.
已知
为坐标原点，
，
（
，
是常数），若
.
（1）求
关于
的函数关系式
；
（2）若
的最大值为
，求的值；
（3）利用（2）的结论，用“五点法”作出函数在长度为一个周期的闭区间上的简图，并指出函数的单调区间.
中，
，试判断平面
与平面
的位置关系，并说明理由．