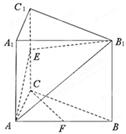
如图,已知直三棱柱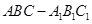 ,
, ,
, 是棱
是棱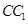 上动点,
上动点, 是
是 中点 ,
中点 , ,
,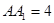 .
.
(1)求证: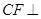 平面
平面 ;
;
(2)当 是棱
是棱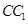 中点时,求证:
中点时,求证: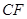 ∥平面
∥平面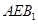 ;
;
(3)在棱 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 的大小是
的大小是 ,若存在,求
,若存在,求 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
(本小题满分12分)某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图5所示,其中120~130(包括120分但不包括130分)的频率为0.05, 此分数段的人数为5人.
(1)问各班被抽取的学生人数各为多少人?
(2)在抽取的所有学生中,任取一名学生, 求分数不小于90分的概率.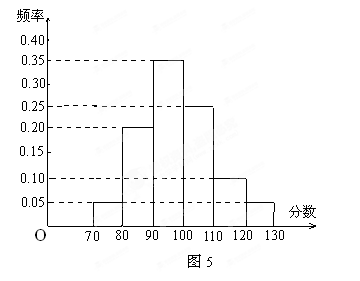
(本小题满分12分)
已知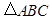 的内角
的内角 所对的边分别为
所对的边分别为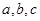 ,且
,且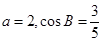 .
.
(1)若 ,求
,求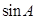 的值;
的值;
(2)若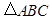 的面积
的面积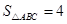 ,求
,求 的值.
的值.
(本小题满分14分)已知函数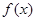 对于任意
对于任意 都有
都有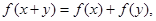 且当
且当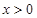 时,有
时,有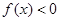 。
。
(1)判断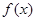 的奇偶性与单调性,并证明你的结论;
的奇偶性与单调性,并证明你的结论;
(2)设不等式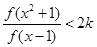 对于一切
对于一切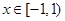 恒成立,求整数
恒成立,求整数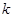 的最小值。
的最小值。
(本小题满分14分)如图所示,某市政府决定在以政府大楼O为中心、正北方向
和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考
虑与周边环境协调,设计要求该图书馆底面矩形的四个顶点都要在边界上,图书馆的正
面要朝市政府大楼.设扇形的半径OM=R ,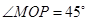 ,OB与OM之间的夹角为
,OB与OM之间的夹角为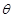 .
.
(1)将图书馆底面矩形ABCD的面积S表示成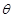 的函数.
的函数.
(2)若 R=45 m,求当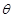 为何值时,矩形ABCD的面积S有最大值?
为何值时,矩形ABCD的面积S有最大值?
其最大值是多少?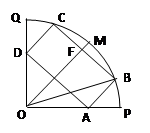
(本小题满分14分)在直三棱柱ABC—A1B1C1中,∠ACB=90°,AC=BC=AA1=1,D、E分别为棱AB、BC的中点,M为棱AA1上的点。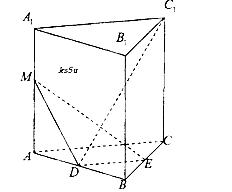
(1)证明:A1B1⊥C1D;
(2)当 的大小。
的大小。