我国是水资源比较贫乏的国家之一，各地采用价格调控等手段来达到节约用水的目的. 某市用水收费的方法是：水费=基本费+超额费+损耗费. 若每月用水量不超过最低限量
时，只付基本费8元和每户的定额损耗费c元；若用水量超过时，除了付同上的基本费和损耗费外，超过部分每1m3付b元的超额费. 已知每户每月的定额损耗费c不超过5元. 该市某家庭今年一月份、二月份和三月份的用水量和支付的费用如下表所示：
根据表格中的数据，求a、b、c.
| 月 份 |
用水量 |
水 费 |
| 一月份 |
9 |
9元 |
| 二月份 |
15 |
19元 |
| 三月份 |
22 |
33元 |
请观察以下三个式子:
①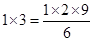
;
②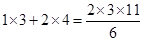
;
③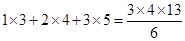
，
归纳出一般的结论，并用数学归纳法证明之.
已知复数
，且
，若
在复平面中对应的点分别为
，求
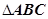的面积.
设函数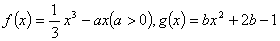
.
(I)若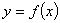曲线
与曲线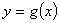
在它们的交点
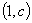处具有公共切线,求
的值;
(II)当
时,若函数
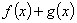在区间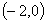
内恰有两个零点,求
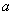的取值范围;
(III)当
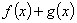时,求函数在区间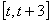
上的最大值
如图，已知椭圆
＝1(a＞b＞0)的离心率为
，以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(
＋1)，一等轴双曲线的顶点是该椭圆的焦点，设P为该双曲线上异于顶点的任一点，直线PF1和PF2与椭圆的交点分别为A、B和C、D.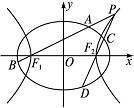 
(1)求椭圆和双曲线的标准方程；
(2)设直线PF1、PF2的斜率分别为k1、k2，证明：k1·k2＝1；
(3)是否存在常数λ，使得|AB|＋|CD|＝λ|AB|·|CD|恒成立？若存在，求λ的值；若不存在，请说明理由．
设函数
，
，
，且以
为最小正周期．
（1）求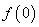
；
（2）求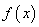
的解析式；
（3）已知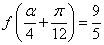
，求
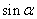的值．