已知直线l:y=k(x+2 与圆O:x2+y2=4相交于A,B两点,O为坐标原点,△AOB的面积为S。(1)试将S表示为k的函数S(k),并求出它的义域;求S的最大值,并求出此时的k值。
与圆O:x2+y2=4相交于A,B两点,O为坐标原点,△AOB的面积为S。(1)试将S表示为k的函数S(k),并求出它的义域;求S的最大值,并求出此时的k值。
(本小题满分13分)已知圆C: 内有一点P(2,2),过点P作直线l交圆C于A、B两点.
内有一点P(2,2),过点P作直线l交圆C于A、B两点.
(1)当l经过圆心C时,求直线l的方程;
(2)当弦AB被点P平分时,写出直线l的方程;
(3)当直线l的倾斜角为45º时,求弦AB的长.
(本小题满分12分)数列{an}中,a1= ,前n项和Sn满足Sn+1-Sn=
,前n项和Sn满足Sn+1-Sn= (n∈N*).
(n∈N*).
(1)求数列{an}的通项公式an以及前n项和Sn;
(2)若S1,t(S1+S2),3(S2+S3)成等差数列,求实数t的值.
(本小题满分12分)已知正四棱锥P-ABCD如图.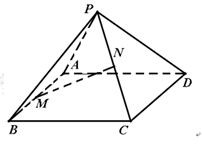
(1)若其正视图是一个边长分别为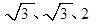 的等腰三角形,求其表面积S、体积V;
的等腰三角形,求其表面积S、体积V;
(2)设AB中点为M,PC中点为N,证明:MN//平面PAD.
(本小题满分12分)在△ABC中,a,b,c分别是A,B,C的对边,且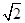 sin A=
sin A=
(1)若a2-c2=b2-mbc,求实数m的值;
(2)若a=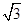 ,求△ABC面积的最大值.
,求△ABC面积的最大值.
(本小题满分12分)已知等比数列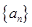 满足
满足 ,数列
,数列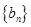 满足
满足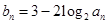 .
.
(Ⅰ)求数列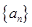 和
和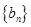 的通项公式;
的通项公式;
(Ⅱ)令 ,求数列
,求数列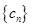 的前n项和
的前n项和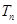 ;
;
(Ⅲ)若 ,求对所有的正整数n都有
,求对所有的正整数n都有 成立的
成立的 的范围.
的范围.