设函数f(x)= a为常数且a∈(0,1).
a为常数且a∈(0,1).
(1)当a= 时,求f
时,求f ;
;
(2)若x0满足f[f(x0)]=x0,但f(x0)≠x0,则称x0为f(x)的二阶周期点.证明函数f(x)有且仅有两个二阶周期点,并求二阶周期点x1,x2;
(3)对于(2)中的x1,x2,设A(x1,f[f(x1)]),B(x2,f[f(x2)]),C(a2,0),记△ABC的面积为S(a),求S(a)在区间[ ,
, ]上的最大值和最小值.
]上的最大值和最小值.
设函数f(x)=ax-(1+a2)x2,其中a>0,区间I={x|f(x)>0}.
(1)求I的长度(注:区间(α,β)的长度定义为β-α);
(2)给定常数k∈(0,1),当1-k≤a≤1+k时,求I的长度的最小值.
如图所示,在多面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,BA⊥AC,ED⊥DG,EF∥DG,且AC=1,AB=ED=EF=2,AD=DG=4.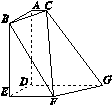
(1)求证:BE⊥平面DEFG;
(2)求证:BF∥平面ACGD;
(3)求二面角F-BC-A的余弦值.
)如图所示,在三棱锥P-ABC中,AB=BC=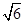 ,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=
,平面PAC⊥平面ABC,PD⊥AC于点D,AD=1,CD=3,PD=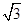 .
.
(1)证明:△PBC为直角三角形;
(2)求直线AP与平面PBC所成角的正弦值.
如图所示,四棱锥P-ABCD的底面ABCD为一直角梯形,其中BA⊥AD,CD⊥AD,CD=AD=2AB,PA⊥底面ABCD,E是PC的中点.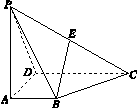
(1)求证:BE∥平面PAD;
(2)若BE⊥平面PCD,求平面EBD与平面BDC夹角的余弦值.