某租赁公司拥有汽车100辆.当每辆车的月租金为3000元时,可全部租出.若每辆车的月租金每增加50元,未租出的车将会增加一辆.租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时, 租赁公司的月收益最大,最大月收益是多少?
某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本 (万元)与年产量
(万元)与年产量 (吨)之间的函数关系式可以近似地表示为
(吨)之间的函数关系式可以近似地表示为 ,已知此生产线年产量最大为210吨.
,已知此生产线年产量最大为210吨.
(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
(本题共2小题,每小题7分,满分14分)设函数 的图象为
的图象为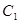 、
、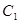 关于点A(2,1)的对称的图象为
关于点A(2,1)的对称的图象为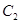 ,
,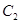 对应的函数为
对应的函数为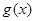 .
.
(1)求函数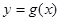 的解析式;
的解析式;
(2)若直线 与
与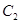 只有一个交点,求
只有一个交点,求 的值并求出交点的坐标
的值并求出交点的坐标
(本题共2小题,每小题6分,满分12分)
已知 ,且
,且
(1)若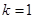 ,求
,求 ;
;
(2)若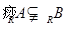 ,求实数
,求实数 的取值范围.
的取值范围.
抛物线 上纵坐标为
上纵坐标为 的点
的点 到焦点的距离为2.
到焦点的距离为2.
(Ⅰ)求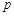 的值;
的值;
(Ⅱ)如图,
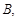
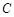 为抛物线上三点,且线段
为抛物线上三点,且线段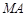 ,
, ,
,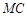 与
与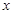 轴交点的横坐标依次组成公差为1的等差数列,若
轴交点的横坐标依次组成公差为1的等差数列,若 的面积是
的面积是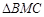 面积的
面积的 ,求直线
,求直线 的方程.
的方程.
已知函数
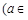 R).
R).
(Ⅰ)若 ,求曲线
,求曲线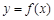 在点
在点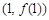 处的的切线方程;
处的的切线方程;
(Ⅱ)若 对任意
对任意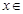
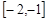 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.