(本题共2小题,每小题6分,满分12分)
已知 ,且
,且
(1)若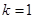 ,求
,求 ;
;
(2)若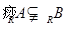 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知数列{an}是等差数列,且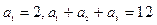
⑴求数列{an}的通项公式
⑵令 ,求数列{bn}的前10项和
,求数列{bn}的前10项和
.已知二次函数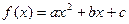 的图象经过点
的图象经过点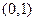 ,
,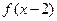 是偶函数,函数
是偶函数,函数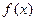 的图象与直线
的图象与直线 相切,且切点位于第一象限
相切,且切点位于第一象限
(Ⅰ)求函数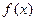 的解析式
的解析式
(Ⅱ)若对一切 ,
, 不等式
不等式 恒成立,求实数
恒成立,求实数 的取值范围
的取值范围
(Ⅲ)若关于x的方程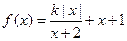 有三个不同的实数解,求实数k的值
有三个不同的实数解,求实数k的值
如图:某污水处理厂要在一个矩形  污水处理池
污水处理池  的池底水平铺设污水净化管道
的池底水平铺设污水净化管道  ,
, 
 是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口
是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口 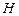 是
是 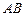 的中
的中  点,
点,  分
分  别落在线段
别落在线段 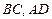 上.已知
上.已知  米,
米, 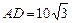 米,记
米,记  .
. 
(Ⅰ)试将污水净化管道的长度  表示为
表示为  的函数
的函数
并写出定义域
(Ⅱ)若 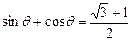 ,求此时管道的长度
,求此时管道的长度 
(Ⅲ)问:当  取何值时,铺设管道的
取何值时,铺设管道的  成本最低?并
成本最低?并  求出此时管道的长度
求出此时管道的长度
已知三次函数 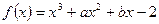 在
在 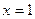 取得极值
取得极值
(Ⅰ)求 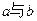 的关系式
的关系式
(Ⅱ)若函数 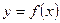 的单调减区间的长度不小于2,
的单调减区间的长度不小于2,  求
求  的取值范
的取值范  围(注:区间
围(注:区间 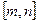 的长度为
的长度为  )
)
(Ⅲ)若不等式  对一切
对一切 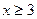 恒成立,求
恒成立,求  的取值范围
的取值范围
在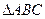 中,
中,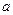 、
、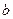 、
、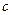 分别为角
分别为角 、
、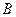 、
、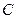 的对边
的对边
已知
(Ⅰ)求角
(Ⅱ)若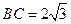 ,内角
,内角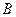 等于
等于 ,周长为
,周长为 ,求
,求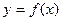 的最大值
的最大值