第一题满分7分,第二题满分7分.
已知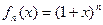 ,
,
(1)若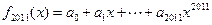 ,求
,求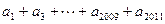 的值;
的值;
(2)若 ,求
,求 中含
中含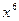 项的系数;
项的系数;
第一题满分5分,第二题满分7分.
已知复数 ,
, =2,
=2,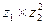 是虚部为正数的纯虚数。
是虚部为正数的纯虚数。
(1)求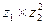 的模;(2)求复数
的模;(2)求复数 。
。
( 14分)已知函数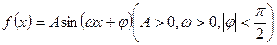 在一个周期内的部分函数图象如图所示.
在一个周期内的部分函数图象如图所示.
(1)( 6分)函数 的解析式.
的解析式.
(2)( 4分)函数 的单调递增区间.
的单调递增区间.
(3) ( 4分)函数 在区间
在区间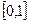 上的最大值和最小值.
上的最大值和最小值.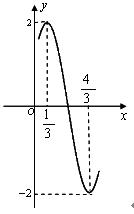
( 12分)已知线段AB的端点B的坐标为(4,3),端点A在圆 上运动,求线段AB的中点M的轨迹方程,并说明M的轨迹是什么图形.
上运动,求线段AB的中点M的轨迹方程,并说明M的轨迹是什么图形.
( 12分)已知集合M={-1,0,1,2},从集合M中有放回地任取两元素作为点P的坐标。
(1)( 4分)写出这个试验的所 有基本事件,并求出基本事件的个数;
有基本事件,并求出基本事件的个数;
(2)( 4分)求点P落在坐标轴上的概率;
(3)( 4分)求点P落在圆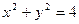 内的概率.
内的概率.