( 14分)已知函数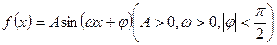 在一个周期内的部分函数图象如图所示.
在一个周期内的部分函数图象如图所示.
(1)( 6分)函数 的解析式.
的解析式.
(2)( 4分)函数 的单调递增区间.
的单调递增区间.
(3) ( 4分)函数 在区间
在区间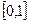 上的最大值和最小值.
上的最大值和最小值.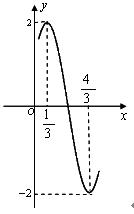
(本小题满分10分)选修4—4:坐标系与参数方程
已知曲线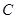 的极坐标方程是
的极坐标方程是 .以极点为平面直角坐标系的原点,极轴为
.以极点为平面直角坐标系的原点,极轴为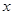 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线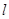 的参数方程是
的参数方程是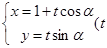 是参数
是参数 .
.
(1)将曲线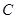 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)若直线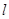 与曲线
与曲线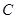 相交于
相交于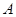 、
、 两点,且
两点,且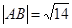 ,求直线的倾斜角
,求直线的倾斜角 的值.
的值.
(本小题满分10分)选修4—1:几何证明选讲
如图所示,PA为圆O的切线,A为切点,PBC是过点O的割线,PA=10,PB=5,∠BAC的平分线与BC和圆O分别交于点D和E.
(1)求证: ;
;
(2)求AD·AE的值.
(本小题满分12分)设函数 .
.
(Ⅰ)若函数 在定义域上为增函数,求实数
在定义域上为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)在(Ⅰ)的条件下,若函数 ,
, 使得
使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知圆 的公共点的轨迹为曲线
的公共点的轨迹为曲线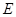 ,且曲线
,且曲线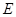 与
与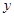 轴的正半轴相交于点
轴的正半轴相交于点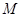 .若曲线
.若曲线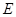 上相异两点
上相异两点 、
、 满足直线
满足直线 ,
,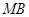 的斜率之积为
的斜率之积为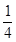 .
.
(Ⅰ)求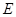 的方程;
的方程;
(Ⅱ)证明直线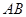 恒过定点,并求定点的坐标;
恒过定点,并求定点的坐标;
(Ⅲ)求 的面积的最大值.
的面积的最大值.
(本小题满分12分)某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.把符合条件的1000名志愿者按年龄分组:第1组[20,25)、第2组[25,30)、第3组[30,35)、第4组[35,40)、第5组[40,45],得到的频率分布直方图如图所示: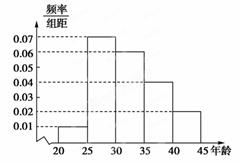
(1)若从第3、4、5组中用分层抽样的方法抽取12名志愿者参加广场的宣传活动,应从第3、4、5组各抽取多少名志愿者?
(2)在(1)的条件下,该市决定在这12名志愿者中随机抽取3名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率;
(3)在(2)的条件下,若ξ表示抽出的3名志愿者中第3组的人数,求ξ的分布列和数学期望.