一条光线从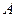 (3,2)发出,经
(3,2)发出,经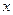 轴反射,通过点
轴反射,通过点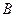 (-1,6),求入射光线和反射光线所在的直线方程.
(-1,6),求入射光线和反射光线所在的直线方程.
在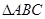 中,已知角
中,已知角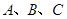 所对的边分别是
所对的边分别是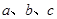 ,边
,边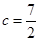 ,且
,且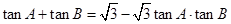 ,又
,又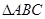 的面积为
的面积为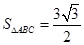 ,求
,求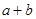 的值.
的值.
(本小题满分14分)
设函数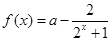 ,
,
(1)求证:不论 为何实数
为何实数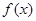 在定义域上总为增函数;
在定义域上总为增函数;
(2)确定 的值,使
的值,使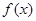 为奇函数;
为奇函数;
(3)当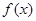 为奇函数时,求
为奇函数时,求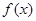 的值域.
的值域.
(本小题满分14分)
某漁业公司年初用98万元购买一艘捕魚船,第一年各种支出费用12万元,以后每年都增加
4万元,每年捕魚收益50万元.
(1)该公司第几年开始获利?
(2)若干年后,有两种处理方案:
①年平均获利最大时,以26万元出售该渔船;
②总纯收入获利最大时,以8万元出售渔船.
问哪种处理方案最合算?
(本小题满分14分)
已知圆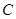 :
: ,直线
,直线 被圆所截得的弦的中点为P(5,3).
被圆所截得的弦的中点为P(5,3).
(1)求直线 的方程;
的方程;
(2)若直线 :
: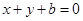 与圆
与圆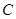 相交于两个不同的点,求b的取值范围.
相交于两个不同的点,求b的取值范围.
(本小题满分14分)
如图,已知正方体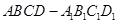 ,
, 是底
是底 对角线的交点.
对角线的交点.
求证:(1) 面
面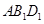 ;
;
(2 ) 面
面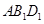 .
. 