口袋中有n(n∈N＊)个白球，3个红球.依次从口袋中任取一球，如果取到红球，那么继续取球，且取出的红球不放回；如果取到白球，就停止取球.记取球的次数为X,若P(X=2)=
求：
（1）n的值；
（2）X的概率分布与数学期望.
（本小题满分12分）
如图，在长方体
中，
P在
上，且
.
1)求证：
2)求二面角
的大小；
3）求点B到平面
的距离.
（本小题满分12分）
在
中,
为其锐角，且
与
是方程
的两个根。
1）求
的值；
2）求函数
在
时的最大值及取得最大值时
的取值.
（本小题满分12分）
甲乙两人进行投篮训练，甲投进的概率为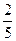
，乙投进的概率为
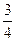，两人投进与否相互没有影响，现两人各投1次，求：
1）甲投进而乙未投进的概率；
2）这两人中至少有1人投进的概率.
如图，在面积为18的△ABC中，AB=5，双曲线E过点A，
|
且以B、C为焦点，已知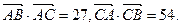
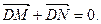
已知等差数列{an}的公差大于0,且a3,a5是方程x2–14x+45 =0的两根,数列{ bn}的前n项的和为Sn，且Sn=1－
（Ⅰ）求数列{an},{bn}的通项公式;（Ⅱ）记cn=anbn,求证cn+1≤cn.
