(本小题满分13分) 设椭圆
设椭圆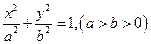 的左右焦点分别为
的左右焦点分别为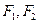 ,离心率
,离心率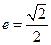 ,过
,过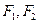 分别作直线
分别作直线 ,且
,且 ,
, 分别交直线
分别交直线 :
: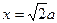 于
于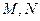 两点。
两点。
(Ⅰ)若 ,求 椭圆的方程;
,求 椭圆的方程;
(Ⅱ)当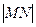 取最小值时,试探究
取最小值时,试探究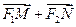 与
与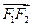
的关系,并证明之.
已知二次函数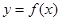 的图像经过坐标原点,其导函数为
的图像经过坐标原点,其导函数为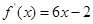 ,数列
,数列 的前n项和为
的前n项和为 ,点
,点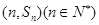 均在函数
均在函数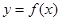 的图像上。
的图像上。
(Ⅰ)、求数列 的通项公式;
的通项公式;
(Ⅱ)、设 ,
, 是数列
是数列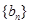 的前n项和,求使得
的前n项和,求使得 对所有
对所有 都成立的最小正整数m;
都成立的最小正整数m;
已知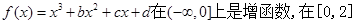 上是减函数,且
上是减函数,且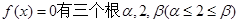 。
。
(1)求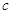 的值,并求出
的值,并求出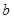 和
和 的取值范围。
的取值范围。
(2)求证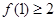 。
。
(3)求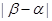 的取值范围,并写出当
的取值范围,并写出当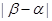 取最小值时的
取最小值时的 的解析式。
的解析式。
设a>0且a≠1, (x≥1)
(x≥1)
(Ⅰ)求函数f(x)的反函数f-1(x)及其定义域;
(Ⅱ)若 ,求a的取值范围。
,求a的取值范围。
设函数 ,已知
,已知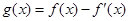 是奇函数。
是奇函数。
(Ⅰ)求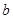 、
、 的值。
的值。
(Ⅱ)求 的单调区间与极值。
的单调区间与极值。
对于定义域为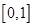 的函数
的函数 ,如果同时满足以下三条:①对任意的
,如果同时满足以下三条:①对任意的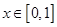 ,总有
,总有 ;②
;② ;③若
;③若 ,都有
,都有 成立,则称函数
成立,则称函数 为理想函数.
为理想函数.
(1) 若函数 为理想函数,求
为理想函数,求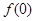 的值;
的值;
(2)判断函数
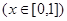 是否为理想函数,并予以证明;
是否为理想函数,并予以证明;
(3) 若函数 为理想函数,
为理想函数, 假定
假定
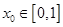 ,使得
,使得 ,且
,且 ,求证:
,求证: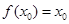 .
.